Wartość bezwględna
Monisiak: Witam, mam problem z tym przykładem. Co robię źle?
|x+1|+1≥x
x+1+1≥x v x+1+1≤−x
2≥0 lub 2x≤−2
x≤−1
Jaka jest odpowiedź? Co nam mówi "2≥0"?
8 kwi 20:08
Benny: 2≥0 oznacza tożsamość, więc dla x∊R nierówność jest spełniona
|x+1|≥x−1, wartość bezwzględna jest nieujemna, więc x−1≥0
dla takich x−ów moim zdaniem rozpatrujemy tylko równanie:
x+1+1≥x
2≥0
ostatecznie x∊<1;+∞)
8 kwi 20:17
Monisiak: No a odpowiedź to liczby Reczywiste. x∊R
Dlatego mam własnie wątpliwości

8 kwi 20:19
Monisiak: Ktoś coś?
8 kwi 20:32
PW: Rozwiązaniami nierówności
2 ≥ 0
są wszystkie liczby rzeczywiste. Nad rozwiązaniem drugiej z nierówności można się już nie
zastanawiać, bo jest to alternatywa nierówności, a nie koniunkcja.
Odpowiedź: rozwiązaniami są x∊R.
Inaczej można się przekonać w ten sposób:
|x+1| ≥ x −1.
Dla x < 1 prawa strona jest liczbą ujemną, a więc nierówność jest spełniona w sposób oczywisty,
bo lewa strona jest z definicji nieujemna.
9 kwi 14:35
Mila:
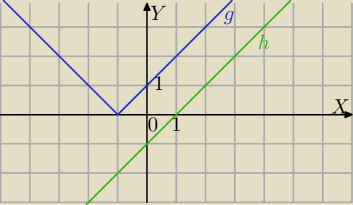 Metoda graficzna:
Metoda graficzna:
|x+1|+1≥x⇔
|x+1|≥x−1
g(x)=|x+1|
h(x)=x−1
Wykres funkcji g(x) leży nad wykresem funkcji h(x) dla każdego x∊R
9 kwi 14:42

 Metoda graficzna:
|x+1|+1≥x⇔
|x+1|≥x−1
g(x)=|x+1|
h(x)=x−1
Wykres funkcji g(x) leży nad wykresem funkcji h(x) dla każdego x∊R
Metoda graficzna:
|x+1|+1≥x⇔
|x+1|≥x−1
g(x)=|x+1|
h(x)=x−1
Wykres funkcji g(x) leży nad wykresem funkcji h(x) dla każdego x∊R