a matematyk: 1.Oblicz drugi wyraz ciągu geometrycznego an określonego wzorem a_n=4^x_n wiedząc że x₅=10 oraz x₁+x₂+...+x₁₂=174 2.Obwód trapezu ABCD jest równy 24. Kąt między ramieniem AD o dł.6 a dłuższą podstawą ma 60 stopni. Przekątna BD trapezu dzieli go na 2 trójkąty których stosunek pól wynosi 3. Oblicz pole trapezu 3. Czworokąt wpisano w okrąg o promieniu 8 i wiadomo że jedna z przekątnych czworokąta ma

	1
długość 8√3, a suma sinusów wszystkich kątów wewnętrznych czworokąta wynosi		.
	√3−√2

Oblicz miarę kątów wewnętrznych

===: ...matematyk ... a gdzie precyzja Co z pełną treścią zadania 1 ?

matematyk: tak brzmi całe polecenie

===: a co to jest x_n

matematyk: ja nic wiecej nie mam zapisane

===: skoro a_n=4^x_n jest ciągiem geometrycznym to łatwo wykazać, że x_n musi być ciągiem arytmetycznym Policzysz łatwo że x₁=−2 r=3 zatem x₂=1 a₂=4

===: poradzisz?

matematyk: a jak to wykazać ze x_n jest ciągiem arytmetycznym?

===: Skoro a_n=4^x_n jest ciągiem geometrycznym to

an+1
	=const
an

4xn+1
	=4xn+1−xn zatem xn+1−xn=const i wniosek
4xn

===: i teraz zabieraj się za ten ciąg arytmetyczny po to aby wyznaczyć x₂ Znając x₂ .... policzysz a₂ −

===: i teraz zabieraj się za ten ciąg arytmetyczny po to aby wyznaczyć x₂ Znając x₂ .... policzysz a₂ −

matematyk: wielkiee dzięki a poradzisz coś z zadaniem 2 i 3?

matematyk: :(

Tadeusz: Widzę, że nie rozbombiłeś − 2) to dość ciekawe zadanko Łatwo wykażesz, że jeśli krótsza podstawa to a to dłuższa 3a Kąt 60^o i ramię trapezu 6 ... czyli wysokość h=3√3 Dalej robiąc rachunek obwodu ustalisz, że a=3 zatem trapez równoramienny. Jego pole to już oczywiście gimnazjum −

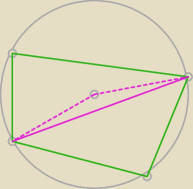
Tadeusz: ... i chyba już widzisz ... policzysz kąt środkowy ... to znasz i wpisany oparty na tym samym łuku. smacznego−