W trapezoidzie połączono środki boków, otrzymując czworokąt.... alexaa: 1. W trapezoidzie połączono środki boków, otrzymując czworokąt KLMN. a) Udowodnij, że czworokąt KLMN jest równoległobokiem. b) Oblicz pole czworokąta KLMN, wiedząc, że przekątne trapezoidu przecinają się pod kątem 30*, a jego pole jest równe 24 cm². 2. W rombie cosinus kąta ostrego jest równy ⁴₅ , a suma dł. boku i wysokości jest równa 8√5 cm. Oblicz: a) dł. przekątnych i boku rombu b) pole rombu. 3. Rozważmy równoległoboki, w których przekątne przecinają się pod kątem 30*, a suma długości tych przekątnych jest równa 12. Wybierz równoległobok o największym polu, wyznacz to pole oraz oblcz dł. boków tego równoległoboku. Proszę o pomoc w tych zadaniach.

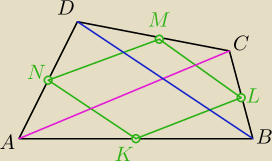
===: 1) nic tu do udowadniania i jak dobrze podumasz nic do liczenia

alexaa: pomoże ktoś dalej?

===: Przekątna AC dzieli Twój trapezoid na ΔACD i ΔACB Jeśli w trójkącie ACD poprowadzisz odcinek łączący środki boków AD i CD to chyba nie trzeba tłumaczyć, że NM jest równoległy do AC (podobieństwo ΔACD i ΔNMD) ... i tak dalej