afs msp: Wewnątrz trójkąta równobocznego o boku długości 100√3 wybrano punk K taki, że jego odległość od dwóch boków trójkąta są równe 19 i 8. Oblicz odległość punktu K od trzeciego boku.

Janek191:

	√3
19 + 8 + x = 100√3*
	2

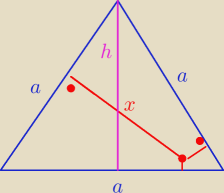
27 + x = 150 x = 123 ====== Korzystamy z wzoru x + y + z = h =========

msp:

	√3
z czego został wzięty ten
	2

msp: już wiem, ale co to za wzór x + y + z =h?

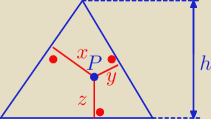
Janek191: Suma odległości dowolnego punktu P leżącego wewnątrz Δ równobocznego od jego boków jest równa wysokości tego Δ. x + y + z = h