najmniejsza wartość pola, parametr girlol: Jaką wartość powinno mieć m aby pole obszaru ograniczonego przez wykresy funkcji y=|x−1|−2 i y=2mx było najmniejsze?

girlol: Wiem, że trzeba porównać te funkcje i później wyjdą z tego dwa punkty przecięcia które w swoich współrzędnych będą miały m. Trzecim wierzchołkiem jest punkt (1,−2). A później ze wzoru na pole trójkąta mając dane wierzchołki. Ale dalej mi nie wychodzi. Nie wiem czy trzeba z pochodnej? Proszę o pomoc.

girlol: Up

Marek216: W tym zadaniu niekoniecznie proste wyznaczą figurę może tak być ale nie musi.

Marek216: Napisz ile już wyliczyłeś, w którym jesteś miejscu.

===:

Marek216: Chodziło mi o to że gdy 2m jest większe lub równe od 1 lub mniejsze lub równe od −1 to nie powstanie figura, wiem jak wykres wygląda.

girlol: 2mx=|x−1|−2 dla x większego lub równego 1 2mx=x−3 x=−3/(2m−1) y=−6m/(2m−1) dla x mniejszego od 1 2mx=−x−3 x=−1/(2m+1) y=−2m/(2m+1) Pole trójkąta: P(m)= 0,5*|[−1/(2m+1) + 3/(2m−1)]*[−2+ 6m/(2m−1)]−[−2m/(2m+1) + 6m/(2m−1)]*[1+ 3m/(2m−1)]| No i tyle. Później wychodzą z tego cuda...

girlol: up

girlol: Pomoże ktoś?

girlol: up

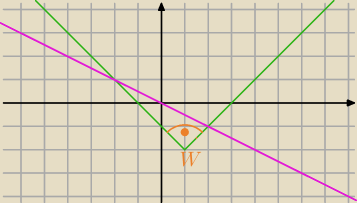
===: Jeśli zauważysz przyprostokątne i policzysz porządnie ich długość jako długość odcinków wyznaczonych przez policzone już przez Ciebie punkty przecięcia i punkt W=(1,−2) ... to wyniki nie są takie cudaczne −

===: powinieneś otrzymać

	2(2m+2)2		2(2m+2)2
√		i √
	(2m+1)2		(2m−1)2

licz pole i szukaj minimum

girlol:

	(2m+2)4
Już tak robiłem, ale nie umiem policzyć pochodnej z
	(2m+1)2(2m−1)2

===: chyba nie zauważyłeś pierwiastków

girlol: No tak. Wszystko powinno być pod pierwiastkiem, ale to będzie jeszcze trudniejsze. Miałem pochodne i tak dalej, ale nigdy nie były takie złożone.

===:

	1		2|2m+2|		|2m+2|		(2m+2)2
S=		*		*		=
	2		|2m+1|		|2m−1|		|4m2−1|