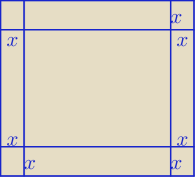
 a = 30 − 2x
Objętość
V = a2*x = ( 30 − 2 x)2*x = ( 900 − 120 x + 4 x2)*x = 4 x3 − 120 x2 + 900 x
więc
V '(x) = 12 x2 − 240 x + 900 = 0
x2 − 20 x + 75 = 0
Δ = 400 − 4*1*75 = 400 − 300 = 100
√Δ = 10
a = 30 − 2x
Objętość
V = a2*x = ( 30 − 2 x)2*x = ( 900 − 120 x + 4 x2)*x = 4 x3 − 120 x2 + 900 x
więc
V '(x) = 12 x2 − 240 x + 900 = 0
x2 − 20 x + 75 = 0
Δ = 400 − 4*1*75 = 400 − 300 = 100
√Δ = 10
| 20 − 10 | ||
x = | = 5 lub x = 15 − odpada , bo 30 − 2*15 = 0 | |
| 2 |