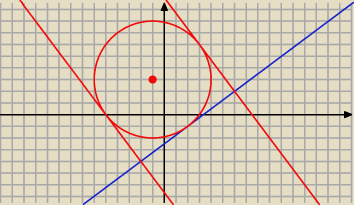
Geometria analityczna Piotrek: Dany jest okrąg o równaniu (x+1)²+(y−3)²=25 oraz prosta o równaniu 4y=3x−10. Wyznacz równania prostych stycznych do okręgu i prostopadłych do danej prostej.

Piotrek: Może ktoś pomóc

Janek191: 4 y = 3 x − 10

	3
y =		x − 2,5
	4

więc prosta prostopadła będzie postaci :

	4
y = −		x + k
	x

i teraz rozwiąż układ równań : x² + 2 x + 1 + y² − 6 y + 9 = 25

	4
y = −		x + k
	3

−−−−−−−−−−−−−−− Δ musi być = 0

Janek191: Miało być

	4
y = −		x + k
	3

Piotrek: I wyszło mi 25x²+x(90−27k)+9k²−54k−135=0 A Δ=−9(19k²−60k−2400) Δ z √Δ=√182000 i to ma jakiś koszmarny pierwiastek I co teraz? Chyba że zrobiłem jakiś błąd?

Janek191: 25 x² + ( 90 − 24 k) x + 9 k² −54 k −135 = 0 Δ = 8 100 − 4 320 k + 576 k² − 900 k² + 5 400 k + 13 500 = = − 324 k² + 1 080 k + 21 600 = 0 / : ( − 4) 81 k² − 270 k − 5 400 = 0 9 k² − 30 k − 600 = 0 3 k² − 10 k − 200 = 0 Δ₁ = 100 − 4*3*(−200) = 100 + 2 400 = 2 500 √Δ₁ = 50

	10 − 50		20
k =		= −		lub k = 10
	6		3

zatem

	4		20		4
y = −		x −		lub y = −		x + 10
	3		3		3