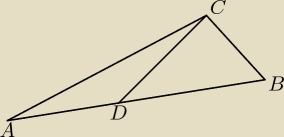
w trójkącie ABC oliwia: w trójkącie ABC bok AC jest 3 razy dłuższy od boku BC. Na boku AB zaznaczono punkt D. Oblicz stosunek pola koła opisanego na trójkącie ADC do pola koła opisanego na trójkącie DBC.

Basia: wykorzystaj wzór

	a
R =
	2sinα

gdzie: R−promień okręgu opisanego α − dowolny kąt a − długość boku leżącego na przeciw kąta α

Ali: za "a" podstawić w pierwszym przypadku AC a w drugim CB ?

Ali: za "a" podstawić w pierwszym przypadku AC a w drugim CB ?

Ali: za "a" podstawić w pierwszym przypadku AC a w drugim CB ?

Ali: przepraszam za SPAM, problemy z przeglądarką

Basia: tak, a odpowiednie kąty to α i 180−α, a sin(180−α) = sinα

Ali: i wynik to (AC)² czyli 9 ? bo reszta się skraca

Basia: wynik to 9, ale nie |AC|², bo |AC| nie znamy wiemy tylko, że |AC|=3|BC|

	|AC|		3|BC|
R1 =		=
	sinα		sinα

	|BC|		|BC|
R2 =		=
	sin(180−α)		sinα

R₁ = 3*R₂

PADC
	=
PDBC

πR12
	=
πR22

9R22
	=9
R22