geometria analityczna okrag
lawenderr: Dane mam okregi styczne zewnetrznie:
O1: (x+2)2 + (y+2)2=20 i O2: (x+1)2 + (y+4)2=5
Oblicz wspolrzedne punktu stycznosci tych okregow.
Wiem, ze nalezy rownania tych okregow przyrownac do siebie, wyrazilam y jako x i podstawilam do
jednego z rownan okregow, otrzymujac rownanie z jedna niewiadoma. Tyle, ze odpowiedz wyszla mi
inna niz wg ksiazki, pomoze ktos? Rachunki juz kilka razy sprawdzalam...
6 kwi 19:17
lawenderr: * okregi te sa oczywiscie styczne WEWNETRZNIE
6 kwi 19:18
Qulka:
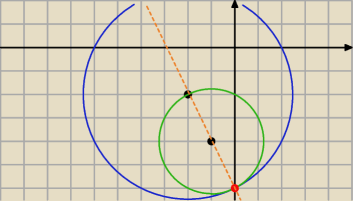
(0,−6)
6 kwi 19:25
Qulka: może łatwiej wyznaczyć prostą przechodzącą przez środki

6 kwi 19:26
Janek191:
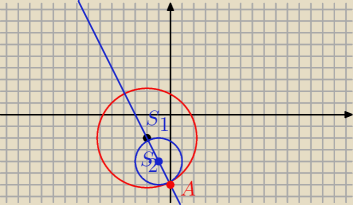
S
1 = ( − 2, −2) S
2 = ( −1 , − 4)
Prosta S
1S
2
y = a x + b
− 2 = − 2a + b
− 4 = − a + b
−−−−−−−−− odejmujemy stronami
2 = − a
a = − 2
b = a − 4 = − 6
y = − 2 x − 6
=========
x
2 + 4 x + 4 + ( − 2 x − 6 + 2)
2 = 20
x
2 + 4 x + 4 + ( − 2 x − 4)
2 = 20
x
2 + 4 x + 4 + 4 x
2 + 16 x + 16 − 20 = 0
5 x
2 + 20 x = 0
5x*( x + 4) = 0
x = 0 lub x = − 4
y = − 2*0 − 6 = − 6
A = ( 0, − 6)
==========
6 kwi 19:26
Marc1n12: Dany jest ciąg (an) określony wzorem: an=3n2−7
a). Wykaż, że ciąg (an) jest rosnący
6 kwi 19:29
lawenderr: Dzieki

6 kwi 21:05
 (0,−6)
(0,−6)

 S1 = ( − 2, −2) S2 = ( −1 , − 4)
Prosta S1S2
y = a x + b
− 2 = − 2a + b
− 4 = − a + b
−−−−−−−−− odejmujemy stronami
2 = − a
a = − 2
b = a − 4 = − 6
y = − 2 x − 6
=========
x2 + 4 x + 4 + ( − 2 x − 6 + 2)2 = 20
x2 + 4 x + 4 + ( − 2 x − 4)2 = 20
x2 + 4 x + 4 + 4 x2 + 16 x + 16 − 20 = 0
5 x2 + 20 x = 0
5x*( x + 4) = 0
x = 0 lub x = − 4
y = − 2*0 − 6 = − 6
A = ( 0, − 6)
==========
S1 = ( − 2, −2) S2 = ( −1 , − 4)
Prosta S1S2
y = a x + b
− 2 = − 2a + b
− 4 = − a + b
−−−−−−−−− odejmujemy stronami
2 = − a
a = − 2
b = a − 4 = − 6
y = − 2 x − 6
=========
x2 + 4 x + 4 + ( − 2 x − 6 + 2)2 = 20
x2 + 4 x + 4 + ( − 2 x − 4)2 = 20
x2 + 4 x + 4 + 4 x2 + 16 x + 16 − 20 = 0
5 x2 + 20 x = 0
5x*( x + 4) = 0
x = 0 lub x = − 4
y = − 2*0 − 6 = − 6
A = ( 0, − 6)
==========
