Pole trojkata galon: Wyznacz pole trójkąta w zależności od długości jego środkowych

galon: ktoś coś?

5-latek:

	s1,+s2+s3
Jeśli p− polowa dlugosci srodkowych czyli p=
	2

	4
to pole trojkata Ptr=		√p(p−s1)(p−s2)(p−s3)
	3

WIdzisz analogie do wzoru Herona ?

galon: analogię widze ciezko byłoby mi to rozpisac potrzebuję skrupulatnego rozwiąznia siedze nad tym zadaniem juz 3 godziny i korzystałam z cartona cosinusa herona ale nie potrafie tego jakos tak skleic

galon: Czy mogę liczyć na Twoją pomoc 5−latek?

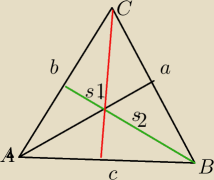
5-latek: Dlugosc srodkowej laczacej wierzchołek A z bokiem a wyraza się wzorem

	1
s1=		√2(b2+c2)−a2
	2

Teraz cyklicznie przestawiasz sobie pod pierwiastkiem i masz s ₂ czyli dlugosc srodkowej laczacej wierzchołek B z bokiem b

	1
s2=		√2(a2+c2)−b2
	2

Teaz oblicz tak samo dlugosc srodkowej s₃

	1
s3=		√2(a2+b2)−c2
	2

Jeszcze masz jedne wzory do tego a²=2(b²+c²−2s₁²) b²= 2(a²+c²−2s₂²) c²= 2(a²+b²−2s₃²) Mysle ze tyle wzorow powinno wystarczyc do policzenia pola gdy masz dane 3 boki

5-latek: I może jeszcze to http://www.google.pl/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0CCAQFjAA&url=http%3A%2F%2Fpl.wikipedia.org%2Fwiki%2F%25C5%259Arodkowa_tr%25C3%25B3jk%25C4%2585ta&ei=n8wiVaDCLoH-sgGgi4HgDA&usg=AFQjCNEgZtbKNZJQ_4C7FS-kwqcI3PHWBA

galon:

	1
tak dla ścisłości s1=		√2(b2+c2)−a2 przedstawia nam to samo co
	2

a²=2(b²+c²−2s₁²)

5-latek: Nie bo s₁ to dlugosc srodkowej natomiast a²− to dlugosc boku a do potęgi drugiej Wiec zauważ ze jeśli znasz dlugosc srodkowej np. s₁ i znając dlugosc bokow b i c możesz obliczyć bok a bo a²= 2(b²+c²−2s₁²) to a= √2(b²+c²−2s₁²)

galon: Chodziło mi bardziej o zapis. Te zdania są równoważne.

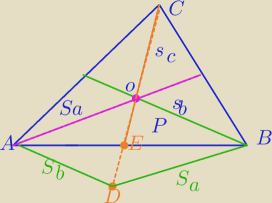
Mila: 1) Trzy środkowe rozcinają trójkąt na sześć części o równych polach. 2) Przedłużam środkową SC w taki sposób, że OE=ED Przekątne czworokąta ADBO dzielą się na połowy, zatem jest równoległobokiem. Oznaczam pole ΔOEB jako P. P_ΔABC=6P

	2		2		2
3) Obliczamy pole ΔODB o bokach :		Sc,		Sb,		Sa
	3		3		3

	2   2   2   Sc+ Sb+ Sa 3   3   3		Sc+ Sb+Sa
p=		=
	2		3

P_ΔODB =2P=√p*(p−Sa)*(s−Sb)*(p−Sc)=

	√(Sa+Sb+Sc)*(Sb+Sc−2Sa)*(Sa+Sc−2Sb)*(Sa+Sb−2Sc)
=		=
	√3*√3*√3*√3

	√(Sa+Sb+Sc)*(Sb+Sc−2Sa)*(Sa+Sc−2Sb)*(Sa+Sb−2Sc)
=
	9

	√(Sa+Sb+Sc)*(Sb+Sc−2Sa)*(Sa+Sc−2Sb)*(Sa+Sb−2Sc)
PΔABC=
	3

Trzeba sprawdzić, czy nie ma pomyłki.

(/-/\-\): Dobrze miła jestes super

Mila:

galon: Dziękuje Mila