Mógłbym liczyć na pomoc z paroma zadankami z fizy? :)
Benny: Wyobraź sobie, że każdy z atomów żelaza w jego kawałku o masie 56g zjonizowano jednokrotnie, a
następnie wszystkie uzyskane z jonizacji elektrony zgromadzono na niewielkim ciele, które
przeniesiono na odległość 1000km od tego kawałka żelaza. Oblicz wartość siły Coulomba, z jaką
kawałek żelaza i ciało, na którym zgromadzone elektrony oddziaływałyby na siebie.
| | g | |
Masa molowa żelaza jest równa 56 |
| |
| | mol | |
Nie za bardzo rozumiem o co chodzi z tą jonizacją i nie wiem jak zabrać się do policzenia
ładunku

q=n*e
6 kwi 18:28
Qulka: czyli masz 1 mol atomów i od każdego zabrano 1 elektron
q=6,023•10
23 •1,66•10
−19C = 10
5C
| | 1010 | |
F=9•109 |
| = 9•107N |
| | 1012 | |
6 kwi 18:32
Benny: Mam rozumieć, że masa nie ma tutaj znaczenia czy jak to z nią jest?
6 kwi 20:11
Qulka: ma znaczenie podzieliłam masę przez masę molową i miałam mole ...
tutaj 56/56 dało 1 mol
6 kwi 20:18
Benny: to mamy tak:
n=1 mol
w 1 molu mamy 6,023*10
23 atomów, więc to jest to dopiero to moje "n" we wzorze na ładunek?

6 kwi 20:45
Qulka: tak
6 kwi 20:54
Benny: Ok, dziękuje

Pocieramy o siebie dwie szklane płytki o takich samych gęstościach, ale różnych rozmiarach,
przy czym płytka 1. jest mniejsza niż płytka 2.
Zdania na prawdę i fałsz.
Płytka 1. naelektryzowała się dodatnio.
Płytka 2. pozostała nienaelektryzowana.
Tylko jedna płytka mogła się naelektryzować.
No i ja myślę, że jeśli mamy dwie szklane płytki to rozmiar i gęstość nie mają wpływu na
naelektryzowanie się więc prawdziwe będzie tylko zdanie nr 3.
6 kwi 21:07
Benny: Qulka, zajrzysz?

6 kwi 21:37
Qulka: na pewno jeśli już to obie są naelektryzowane i zdecydowanie różnoimiennie, tyle że obie tak
samo chetnie trzymają elektrony a rozmiar niekoniecznie ma tu znaczenie
6 kwi 21:44
Benny: W odpowiedziach jest
1.F
2.P
3.F
więc teraz to już nie mam pojęcia jak to będzie
6 kwi 21:48
Qulka: no to słusznie zakładałam że nic się nie stanie
6 kwi 21:49
Qulka: tyle że dziwiło mnie takie rozbicie na płytki bo to obie będą nienaelektryzowane
6 kwi 21:50
Benny: A czemu tak się dzieje? Nie powinno być tak, że jak obie mają ładunek obojętny to z jednej
przejdą elektrony na drugą?
6 kwi 21:52
Qulka: jak obie szklane to żadna nie odda, bo tak samo mocno trzymają
6 kwi 21:53
Benny: więc tak samo będzie się działo, gdy np. będziemy pocierać ebonit o ebonit? aby był przeskok
elektronów musi być pocieranie o inny materiał?
6 kwi 21:57
Qulka: tak
6 kwi 21:59
Benny: Okej

Dwie kulki stalowe o takiej samej średnicy umieszczono na statywach wykonanych z izolatora i
wielokrotnie elektryzowano ładunkiem tego samego znaku w taki sposób, że ich łączny ładunek Q
był za każdym razem jednakowy.
W jaki sposób powinien być rozdzielony ładunek Q między kulami, aby po naładowaniu siła
oddziaływania między nimi dla danej odległości osiągnęła maksymalną wartość?
No to moim zdaniem siła oddziaływania będzie największa, jeśli Q
1=Q
2
6 kwi 22:07
Qulka: jak znam życie to tak

o czym świadczą wszystkie zadania optymalizacyjne

6 kwi 22:10
Benny: No właśnie tak mi się skojarzyło z optymalizacją, a zawsze jest tak, że np. pole figury jest
największe dla równych boków

6 kwi 22:12
Benny: A jeszcze trzeba zapisać zależność F(q1) to co mam tutaj zapisać?
6 kwi 22:13
6 kwi 22:23
Benny: Jej, więc chodziło tylko o zapisanie tej funkcji dzięki której wyznaczymy q
1=q
2?

6 kwi 22:26
Qulka: tak
6 kwi 22:29
daras: 2 płytki szkalne możemy pocierać do usranej śmierci i sie nie naelektryzuja od siebie
musza być 2 różne ciała

kto wymyśla te głupie pytania

6 kwi 22:41
daras: może autor wyjaśni jak je "wielokrotnie" naelektryzował?
tak q1 = q2 bo wtedy F = Fmax
6 kwi 22:43
Benny: próżnia 1
powietrze 1,00059
olej silikonowy 2,5
alkohol metylowy 30
woda destylowana(nie mogę się rozczytać 50 lub 60)
W których z wymienionych ośrodków wartość siły oddziaływania między kulkami jest największa?
Odpowiedź uzasadnij, powołując się na odpowiednie zależności.
więc jeśli ε
r rośnie to siła również rośnie
Siła oddziaływania będzie największa w wodzie destylowanej.
Dobrze?
6 kwi 22:44
daras: woda 81
6 kwi 22:46
daras: | | 1 | |
w próżni bo nie ma czynnika |
| |
| | ε | |
6 kwi 22:47
6 kwi 22:49
Benny: Nie za bardzo rozumiem.
6 kwi 22:49
Benny: To jak mam to wyjaśnić?

6 kwi 22:50
daras: niby czego nie rozumiesz

tylko konkretnie

6 kwi 22:50
daras: zapoznaj sie dobrze ze wzorem najpierw na siłę Coulomba,
to może zrozumiesz
6 kwi 22:51
Qulka: we wzorze na k jest ε =ε0•εr
tylko dla próżni tam jest ε0
6 kwi 22:56
Benny: Ajjj no faktycznie, bo na wikipedii na coś innego chyba popatrzyłem i pomieszały się dwa wzorki

6 kwi 23:06
Benny: ε=ε
0*ε
r
więc odwrotnie jak napisałem wcześniej
im mniejszy mianownik tym większa siła, mianownik najmniejszy dla ε=ε
0, więc największa siła
będzie w próżni
6 kwi 23:58
7 kwi 18:12
daras: nie ma kulki
jest
daras
treść zadań przepisujemy tutaj
bo ani kulce ani nikomu
innemu
nie
chce
się
kręcić szyją
żeby je
odcyfrować
7 kwi 18:14
Benny: Tylko, że tam jest rysuneczek

7 kwi 18:15
daras: PS. nie dość , że na rysunku nic nie widać, to
zadanie
jest
z
cyklu
tych
banalnych

Po prostu
zastosuj
dobrze
ci znana

?
ZASADĘ SUPERPOZYCJI NATĘŻEŃ

7 kwi 18:16
Benny: Coś chyba źle podstawiam, bo wynik mi się nie zgadza z odpowiedzią, a zdjęcia sam takie
dostałem

7 kwi 18:18
daras: a jakie masz wyniki?
przedstaw TUTAJ swój sposób rozwiązania
7 kwi 18:28
Benny: E
w=E
1−E
2
no i coś jest już nie tak, ponieważ jak odejmę to nie wychodzi jak w odp.czyli 16/27
7 kwi 18:46
Benny: I gdzie tu jest błąd?

7 kwi 19:01
Benny: Qulka zajrzysz?
7 kwi 22:05
Qulka: kula nie jest jednorodna i musisz znaleźć środek ładunku i od niego liczyć R
7 kwi 22:28
Benny: No to teraz już całkiem nie wiem

7 kwi 22:31
Qulka: poza tym mała jest w odległości 3/2R od punktu S
7 kwi 22:37
Benny: Tak, wiem tam miałem błąd, ale nie wiem jak się zabrać za tą duża kulę

7 kwi 22:39
Qulka: jeśli małej wychodzi 2/27 to duża musi mieć 2/3 czyli musiałby być jakiś
√7 w tej Rce

7 kwi 22:53
Benny: | | √7 | |
No, gdyby podstawić do odpowiedzi to ta odległość dużej do S wychodzi |
| |
| | 2 | |
7 kwi 22:58
Benny: Tylko jak to policzyć?

7 kwi 22:58
Qulka: normalnie to całkami

ale to chyba za wcześnie

7 kwi 23:02
Benny: No w liceum nie mamy całek, ale nauczyć się nie zaszkodzi

7 kwi 23:04
7 kwi 23:05
Qulka: tak łatwiej

7 kwi 23:05
Benny: To musimy znaleźć środek masy dużej kuli i małej i odjąć czy jak?
7 kwi 23:10
7 kwi 23:15
Qulka: no i będzie
√7 
7 kwi 23:21
Benny: Dodaje i dziwne liczby mi wychodzą

7 kwi 23:25
Qulka:
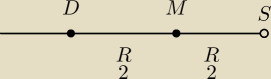
x=
√9/8R
7 kwi 23:28
Qulka: nadal wynik dla E=26/27
7 kwi 23:33
Benny: no właśnie podstawiłem ten pierwiastek i po odjęciu wyszło 26/27
Możesz wyjaśnić czemu to równanie tak zapisałaś?
7 kwi 23:36
Qulka: bo tak naprawdę liczymy środek ładunku nie masy więc pomnożyłam przez ρ i wszystkie stałe
zastąpiłam jednym Q

liczę odległości od S (bo to mi potem będzie potrzebne
i tak jak napisali w książce wydrążenie się odejmuje
7 kwi 23:48
Benny: ale tam powinno wyjść 16/27 a nie 26/27

7 kwi 23:53
Qulka: nie mam więcej pomysłów ..może jutro coś wymyślę
7 kwi 23:56
Benny: Ja też się dziś poddaję, jeśli chcesz możesz podać też to z całkami, zobaczę to sobie.
Dziękuje za pomoc, dobranoc

7 kwi 23:58
Benny: Qulka, masz siły aby jeszcze raz na spokojnie na to spojrzeć?

8 kwi 21:42
Qulka: popróbuję
8 kwi 21:58
Benny: Dziękuje

8 kwi 21:59
Qulka: policzyłam bezwładność tam powinno być bez kwadratów
8 kwi 22:40
Qulka: tak porządnie Vmałej = 1/8Vdużej więc Q małej = 1/8Q dużej
x=13R/12
8 kwi 22:47
Qulka: błąd ..miałam liczyć bez wydrążenia
QR − 1/8QR/2 = 7/8Qx
x= 15R/14
8 kwi 22:50
daras: dzisiaj wziąłem lupę i dojrzałęm jeda prawidłowość: wszystko leży w jednej linii
i kulka i wnęka więc zadanei jest banalne
8 kwi 22:54
Benny: | | 15R | |
sprawdziłem dla tego x= |
| i nadal inny wynik  |
| | 14 | |
8 kwi 23:09
Qulka: wiem też mi wyszło

8 kwi 23:10
Qulka: policz na natężeniach

| | kQ | | 4kQ | | 4kQ | | 8kQ | |
E= |
| − |
| − |
| = |
| |
| | R2 | | 8R2 | | 8•9R2 | | 18R2 | |
| | 8k4πR3ρ | | 16kπRρ | |
|
| = |
| |
| | 3•18R2 | | 27 | |
8 kwi 23:49
Benny: Jak takie natężenia?
9 kwi 06:58
Qulka: duża kulka pełna − dziura w dużej kulce − mała kulka bo pcha w przeciwną stronę
9 kwi 10:11
daras: ładunki na kulach:
| | 4 | | R | | 7 | |
Q1 = ρV1 = ρ |
| π[R3−( |
| )3] = |
| πρR3 |
| | 3 | | 2 | | 6 | |
| | 4 | | R | | ρπR3 | |
Q2 = ρV2 = ρ |
| π( |
| )3 = |
| |
| | 3 | | 2 | | 6 | |
| | Q1 | | Q2 | |
wypadkowe natężenie E = |E1 − E2| = k[ |
| − |
| ] = |
| | R2 | | (2R−R/2)2 | |
| | k | | 4Q2 | | 177 | |
= |
| [Q1 − |
| ] = ... = kπρR |
| |
| | R2 | | 9 | | 162 | |
9 kwi 10:57
daras: wróć

trzeba jeszcze odjąć to co ubyło czyli ładunek wnęki:
E = | E
1 − E
2 − E
2'| , gdzie E
2' − natężenie brakującej wnęki
korzystamy oczywiście z ZASADY SUPERPOZYCJI

| | kρπR3 | | 4 | | 1 | | 1 | | 5 | |
E = |
| [ |
| − |
| − |
| ] = |
| kρπR |
| | R2 | | 3 | | 6 | | 3 | | 6 | |
9 kwi 11:11
daras: Jednak wynik jest dobry.
ładunki policzyłem też dobrze z tym, że walnąłem się w natężeniach:
Wypadkowe natężenie w pkt. S składa się z sumy wektorowej:
E
1 −wektora natężenia od pełnej kuli o promieniu R w odległości od S równej też jej
promieniowi R
| | R | |
E2 − wektora natężenia od wydrążenia w odległości od S równej r = |
| |
| | 2 | |
| | 3 | |
E2' − wektora natężenia od kulki o promieniu r w odległości od S równej 2R−r= |
| R |
| | 2 | |
Zasada superpozycji: wszystkie wektory są współliniowe z tym, że oba wektory E−2 mają zwrot
przeciwny do wektora E
!
więc przechodząc do r−nia skalarnego mamy:
E = E
1 − E
2 − E
2'
| | k | | 4 | | k | | 1 | | k | | 1 | |
E = |
| * |
| πR3ρ − |
| * |
| πR3ρ − |
| * |
| πR3ρ = |
| | R2 | | 3 | | (R/2)2 | | 6 | | (3R/2)2 | | 6 | |
| | 2 | | 2 | | 16 | |
= kπRρ [ |
| − |
| ] = |
| kπRρ  |
| | 3 | | 27 | | 27 | |
9 kwi 11:56
daras: PS. gorąca prośba:
problemy fizyczne wstawiaj na fizyczny.pisz.pl
niech ludzie, którzy TYLKO kopiują i wklejają TAM zadania domowe, po czym czekają na zmiłowanie
zobaczą, że można samemu próbować dochodzić do rozwiązań, może się to im przyda ?
a tutaj wszystko ginie w powodzi problemów czysto matematycznych
9 kwi 12:07
Benny:
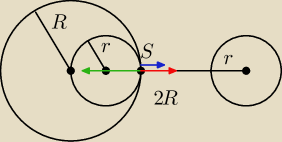
Dziękuje

W szkole jeszcze raz na to spojrzałem i udało mi się do tego dojść.
Wektor zielony E
1
wektor czerwony E
2
wektor niebieski wektor E
2'
| | 4 | | R | | 2 | |
E2=k* |
| *π*( |
| )3*ρ*( |
| )2 |
| | 3 | | 2 | | R | |
| | 4 | | R | | 2 | |
E2'=k* |
| *π*( |
| )3*ρ*( |
| )2 |
| | 3 | | 2 | | 3R | |
E=E
1−E
2−E
3
| | 4 | | 2 | | 2 | |
E=k*π*R*ρ( |
| − |
| − |
| ) |
| | 3 | | 3 | | 27 | |
może być?
wektory dobrze?
9 kwi 16:05
daras: tak, jeżeli zakładasz, że kulki są naładowane ujemnie
9 kwi 16:52
 q=n*e
q=n*e

 Pocieramy o siebie dwie szklane płytki o takich samych gęstościach, ale różnych rozmiarach,
przy czym płytka 1. jest mniejsza niż płytka 2.
Zdania na prawdę i fałsz.
Płytka 1. naelektryzowała się dodatnio.
Płytka 2. pozostała nienaelektryzowana.
Tylko jedna płytka mogła się naelektryzować.
No i ja myślę, że jeśli mamy dwie szklane płytki to rozmiar i gęstość nie mają wpływu na
naelektryzowanie się więc prawdziwe będzie tylko zdanie nr 3.
Pocieramy o siebie dwie szklane płytki o takich samych gęstościach, ale różnych rozmiarach,
przy czym płytka 1. jest mniejsza niż płytka 2.
Zdania na prawdę i fałsz.
Płytka 1. naelektryzowała się dodatnio.
Płytka 2. pozostała nienaelektryzowana.
Tylko jedna płytka mogła się naelektryzować.
No i ja myślę, że jeśli mamy dwie szklane płytki to rozmiar i gęstość nie mają wpływu na
naelektryzowanie się więc prawdziwe będzie tylko zdanie nr 3.

 Dwie kulki stalowe o takiej samej średnicy umieszczono na statywach wykonanych z izolatora i
wielokrotnie elektryzowano ładunkiem tego samego znaku w taki sposób, że ich łączny ładunek Q
był za każdym razem jednakowy.
W jaki sposób powinien być rozdzielony ładunek Q między kulami, aby po naładowaniu siła
oddziaływania między nimi dla danej odległości osiągnęła maksymalną wartość?
No to moim zdaniem siła oddziaływania będzie największa, jeśli Q1=Q2
Dwie kulki stalowe o takiej samej średnicy umieszczono na statywach wykonanych z izolatora i
wielokrotnie elektryzowano ładunkiem tego samego znaku w taki sposób, że ich łączny ładunek Q
był za każdym razem jednakowy.
W jaki sposób powinien być rozdzielony ładunek Q między kulami, aby po naładowaniu siła
oddziaływania między nimi dla danej odległości osiągnęła maksymalną wartość?
No to moim zdaniem siła oddziaływania będzie największa, jeśli Q1=Q2
 o czym świadczą wszystkie zadania optymalizacyjne
o czym świadczą wszystkie zadania optymalizacyjne 


 kto wymyśla te głupie pytania
kto wymyśla te głupie pytania 

 tylko konkretnie
tylko konkretnie


 Po prostu
zastosuj
dobrze
ci znana
Po prostu
zastosuj
dobrze
ci znana ?
ZASADĘ SUPERPOZYCJI NATĘŻEŃ
?
ZASADĘ SUPERPOZYCJI NATĘŻEŃ 






 ale to chyba za wcześnie
ale to chyba za wcześnie 




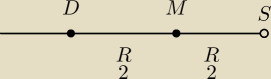
 liczę odległości od S (bo to mi potem będzie potrzebne
i tak jak napisali w książce wydrążenie się odejmuje
liczę odległości od S (bo to mi potem będzie potrzebne
i tak jak napisali w książce wydrążenie się odejmuje








 trzeba jeszcze odjąć to co ubyło czyli ładunek wnęki:
E = | E1 − E2 − E2'| , gdzie E2' − natężenie brakującej wnęki
korzystamy oczywiście z ZASADY SUPERPOZYCJI
trzeba jeszcze odjąć to co ubyło czyli ładunek wnęki:
E = | E1 − E2 − E2'| , gdzie E2' − natężenie brakującej wnęki
korzystamy oczywiście z ZASADY SUPERPOZYCJI 

 Dziękuje
Dziękuje  W szkole jeszcze raz na to spojrzałem i udało mi się do tego dojść.
Wektor zielony E1
wektor czerwony E2
wektor niebieski wektor E2'
W szkole jeszcze raz na to spojrzałem i udało mi się do tego dojść.
Wektor zielony E1
wektor czerwony E2
wektor niebieski wektor E2'