Okręgi
Ligia22: Prosta o równaniu x+y=r jest styczna do okręgu o równaniu x2+y2=r. Uzasadnij, ze wówczas r=2.
6 kwi 18:01
daras: skoro jest styczna, to kąt miedzy promieniem a prostą = 90o
6 kwi 18:02
Ligia22: I co dalej?
6 kwi 18:04
daras: skoro wiesz, to działaj
6 kwi 18:08
Qulka:
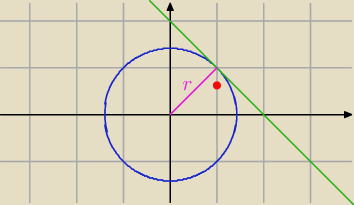
6 kwi 18:12
Ligia22: x+y=2
X2+y2=r
Co dalej?
6 kwi 18:14
ICSP: Pierwszy sposób :
Odległość środka okręgu od równania stycznej powinna być równa promieniowi.
Poszukaj wzoru na odległość prostej od punktu
Drugi sposób:
Rozwiązać układ równań. Podczas rozwiązywania natrafimy na pewne równanie kwadratowe
które powinno mieć tylko jedno rozwiązanie (przecież styczna tylko styka się z okręgiem, a nie
przecina go). Równanie kwadratowe ma jedno rozwiązanie gdy Δ =0. Dostaniesz w ten sposób pewne
równanie z "r" które po rozwiązaniu powinno dać r = 2.
6 kwi 18:15
Ligia22: Ale w tym równaniu mam 3 niewiadome...
6 kwi 18:19
ICSP: w układzie równań

Nic nie szkoda. W warunku Δ = 0 zostanie już tylko jedna.
6 kwi 18:20
Qulka: ale liczysz tylko delta=0 a w delcie będziesz miała tylko r
6 kwi 18:21
daras: ona nawet r−nia okregu nie umie przepisać
dajmy spokój

6 kwi 22:37

 Nic nie szkoda. W warunku Δ = 0 zostanie już tylko jedna.
Nic nie szkoda. W warunku Δ = 0 zostanie już tylko jedna.
