Kula i ostrosłupy Stupid: W kulę o promieniu r wpisujemy ostrosłupy prawidłowe trójkątne w ten sposób, że wierzchołek ostrosłupa jest środkiem kuli, zaś wierzchołki podstawy należą do powierzchni kuli. Wyznacz długość krawędzi podstawy tego ostrosłupa, którego objętość jest największa. Chodzi mi głównie o wyprowadzenie, a nie liczenie pochodnych. W kulę o promieniu r wpisujemy ostrosłupy prawidłowe czworokątne w ten sposób, że wierzchołek ostrosłupa jest środkiem kuli, zaś wierzchołki podstawy należą do powierzchni kuli. Napisz wzór funkcji opisującej objętość V(x) ostrosłupa w zależności od długości krawędzi x jego podstawy. Wyznacz maksymalną objętość ostrosłupa.

Stupid: Podbijam, gdyż mam z tym ogromny problem.

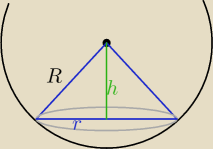
Qulka: h²+r²=R² V=πr²h/3 = π(R²−h²)h/3 i pochodna i =0

Stupid: Podziękował, bo nie wiedziałem jak wyprowadzić.

kix: Idea rozwiązywania będzie taka sama, ale zamień stożek na ostrosłup

Qulka: jak ja tam zobaczyłam stożki to nie wiem... chyba zadanie wcześnej było

	a√3
to jeszcze trzeba potem zamienić że r =
	3

kix: zamienić miał zainteresowany

Stupid: Nie macie się co martwić zauważyłem