wartość bezwględna |2|x-1|-3|≤5 Monisiak: Jeszcze jeden problemik z wartością bezwględną |2|x−1|−3|≤5 2|x−1|−3≤5 v 2|x−1|−3≥−5 2|x−1|≤8 v 2|x−1|≥−2 |x−1|≤4 v |x−1|≥−1 x−1≤4 i x−1≥−4 x−1≥−1 i x−1 ≤1 x≤5 i x≥−3 x≥0 i x≤2 Teraz rysuje te przedziały x∊<−3;5> oraz x ∊<0;2> I czesc wspolna by wynosiła <0;2> Natomiast odpowiedź wynosi <−3;5> Dlaczego?

kix: nierówność ma być spełniona łącznie, wiec nie lub tylko i winno być

Qulka: w drugim przypadku |coś| ≥ −1 dla dowolnego cosia

Monisiak: Aha.... A skąd mam wiedzieć kiedy ma być to co sie pokrywa, a kiedy to co się jakby juz w sobie zawiera? Tzn skad mam wiedzieć kiedy odp. będzie wynosić np. <0;−2> (czyli to co się pokrywa) a nie to co się też w sobie zawiera (czli <−3;5>)? Czy to jest zależne od tego czy mam znak "=" lub "≤" lub "≥"?

Qulka: tablice matematyczne maturalne pierwsza strona jak |coś| < r to część wspólna (i) jak |coś| > r to suma (lub)

kix: po wyjaśnieniu Qulki chyba wszystko już jasne

Qulka: ostatnio wpadłam ma pomysł żeby sobie przewracać nierówność o 90° zgodnie ze wskazówkami zegara jak |coś| < r to i (∧) jak |coś| > r to lub (∨)

Monisiak: A jak są znaki ≥;≤ ? Wzoruję się na kolejnym przykladzie |3−|x+5|| ≤ 1 I wychodzi mi x≥−3 i x≤−7 oraz x≤−1 i x≥−9 Ja bym napisała, że x należy od <−9;−7> suma <−3;−1> a idąc Twoim tokiem rozumowania to by było (−∞;∞) bo jest znak ≤ czyli część wspolna, czyli wszystkie liczby z tych przedziałów. Nie do końca rozumiem

Monisiak: Heh i też takim sposobem robiłam

Qulka: część wspólna to oba jednocześnie razem

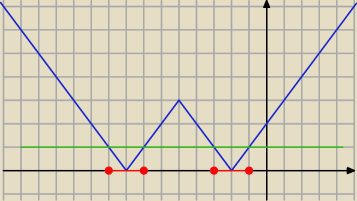
Qulka: i dobrze <−9;−7> u <−3;−1>

Monisiak: Dalej nie rozumiem W tym pierwszym przykładzie jest znak ≤ więc część wspólna, czyli i <−3;5> i <0;2> ==> odp; <−3;5> Nastomiast w kolejym przykładzie |3−|x+5|| ≤ 1 też jest znak ≤ i częścią wspolną by należały wszystkie liczby od x≥−3 i x≤−7 oraz x≤−1 i x≥−9 − z czego odp by wyniosła (−∞;∞) bo w tych przedziałach wszystkie liczby się znajdują. A prawidłowa odpowiedź to <−9;−7> suma <−3;−1>

Qulka: tam jest cześć wspólna z SUMY i iloczynu ( x≥−3 LUB x≤−7 ) CZĘŚĆ WSPÓLNA ( x≤−1 i x≥−9)

Monisiak: Aaaaa teraz jasne Dziękuję!

Qulka:

kix: jeszcze raz, w/g Monisiak rozwiązaniem były x≥ 0 i x≤ 2 a powinno być x ≥ 0 LUB x ≤ 2

Monisiak: Czyli 2|x−1|≤8 v 2|x−1|≥−2 |x−1|≤4 v |x−1|≥−1 x−1≤4 i x−1≥−4 x−1≥−1 LUB x−1 ≤1 x≤5 i x≥−3 x≥0 LUB x≤2 Zgadza sie? To jest pierwszy przyklad

kix: pięknie

Qulka: 2|x−1|≤8 ∧ 2|x−1|≥−2 |x−1|≤4 ∧ |x−1|≥−1 x−1≤4 i x−1≥−4 x∊R x≤5 i x≥−3

kix: ale jest małe ale 2|x−1|≤8 ∧ 2|x−1|≥−2 reszta jest OK

Monisiak: Dziękuję ślicznie

Qulka: jakie OK kix

kix: domyślnie przyjąłem Twoje tłumaczenie z | coś | ≥ −1 za oczywistą oczywistość ( w rozumie cokolwiek podstawiam za x to i tak będzie spełnione )

Qulka: ale ona tego nie uwzględniła w swoim rozwiązaniu

kix: Ty masz dużo większy ikspiriens, więc z pokorą sypię głowę popiołem, chociaż wydawało mi się że załapała