Geometria analityczna okrag
lawenderr: Okrąg przechodzi przez punkt A(4,1), zaś jego środek należy do prostej k: x−y=0. Wiedząc, że
okrąg ten jest styczny do prostej l: y−5=0, wyznacz jego równanie.
Wiec mam takie pytanie, bo zadanie rozwiazalam, ale nie rozumiem jednej rzeczy, prosilabym o
wyjasnienie
. Jezeli srodek okregu S(a,b) nalezy do prostej y=x to wowczas srodek ten ma
wspolrzedne S(a,a). Czy w zwiazku z tym moge napisac, ze promien okregu r
2=a
2=b
2 ? Moim
zdaniem tak, bo okrag jest wowczas styczny do osi ukladu wspolrzednych, jednak wg odpowiedzi
promien nie jest rowny a ani b. Dlaczego?
Janek191:
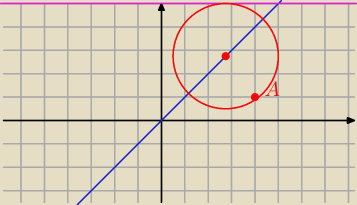
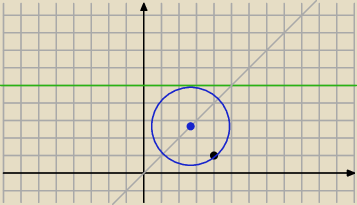
S = ( x, y) = ( x, x)
B = ( x, 5)
A = ( 4, 1)
Mamy
I SA I = I SB I ⇒ I SA I
2 = I SB I
2
( 4 − x)
2 + ( 1 − x)
2 = ( 5 − x)
2 ,
16 − 8 x + x
2 + 1 − 2 x + x
2 = 25 − 10 x + x
2
x
2 = 8
x = 2
√2
S = ( 2
√2, 2
√2)
r
2 = I SB I
2 = 25 − 10*2
√2 + (2
√2)
2 = 25 − 20
√2 + 8 = 33 −20
√2
Równanie okręgu:
( x − 2
√2)
2 + ( y − 2
√2)
2 = 33 − 20
√2
===============================
