3 noc pełna cyferek Spirit: Trochę łatwiejsze od poprzedniego. Może ktoś wie... "Wykres funkcji f(x) = ¹_x został przesunięty w taki sposób, że jego osiami symetrii są proste o równaniach y = x − 7 oraz y = −x−3. Po tym przekształceniu wzór funkcji ma postać y = ¹_{x − p} +q. Wyznacz p i q."

5-latek:

	1
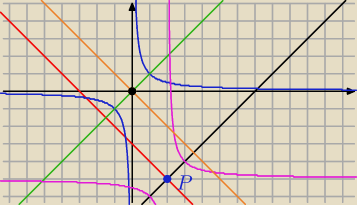
Osiami symetrii hiperboli równoosiowej		sa proste o równaniu y=x i y=−x (zielona i
	x

brazowa Przecinaja się one w punkcie (0,0) Natomiast proste y= x−7 (czarna i y=−x−3 (czerwona które maja być osiami symetrii

	1
przesuniętego wykresu y=		przecinają się w punkcie P=(2−5)
	x

	1
Wiec jak z rysnku widać należy wykres niebieski y=		przesunąć o dwa w prawo i 5 w dol
	x

i otrzymamy wykres rozowy Wiec p=...ile ? i q= ile ?

5-latek:

	1
Oczywiście hiperboli równoosiowej y=		bo to jest funkcja
	x

Spirit: −5, 2. Dziękuję.