a Dark1: Wyznacz wszystkie liczby naturalne dodatnie k , dla których równanie x² + x + 1 = k² ma pierwiastki będące liczbami całkowitymi. Jak to zrobić?

Qulka: tylko dla k=1

Dark1: Jak to zrobić?

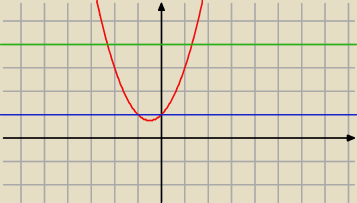
5-latek: y=1² y=2² itd.

Dark1: A bez wykresu?

Dark1: 5 latek i tak mam sprawdzać do nieskończoności?

5-latek: A czy nie możesz pomyslec ? równanie x²+x+1 =0 posiada dwa pierwiastki całkowite x₁= −1 i x₂=0 Teraz mamy wyznaczyć takie k ∊N dla których równanie x²+x+1=k² ma pierwiastki całkowite wiec x²+x+1−k²=0 Rownanie tej postaci będzie miało pierwiastki całkowite gdy będzie postaci x²+x=0 bo x(x+1)=0 to x=0 lub x=−1 to ile musi wynosic k (pamiętaj ze musi być naturalne

5-latek: Być może ktoś jeszcze wytłumaczy inaczej

Godzio:

	√3		√3
Δ = 1 − 4 + 4k2 = 4k2 − 3 ≥ 0 ⇒ k ∊ (−∞, −		) U (		,∞)
	2		2

p[Δ} = √4k² − 3 Żeby w ogóle mówić o pierwiastkach całkowitych, delta musi się pierwiastkować, stąd: 4k² − 3 = p² 4k² − p² = 3 (2k − p)(2k + p) = 3 mamy iloczyn liczb całkowitych, który ma dać 3, możliwe kombinacje: 2k − p = 1 2k + p = 3 ⇒ k = 1, p = 1 2k − p = −1 2k + p = −3 ⇒ k = −1 −− odrzucamy 2k − p = 3 2k + p = 1 ⇒ k = 1, p = −1 −− odrzucamy 2k − p = −3 2k + p = −1 ⇒ k = −1 −− odrzucamy Sprawdzamy co się dzieje dla k = 1 √Δ = 1

	−1 + 1
x1 =		= 0
	2

	−1 − 1
x2 =		= −1
	2

Zgadza się, odp: k = 1

Dark1: Dzięki chłopaki