..
Bershka: 2tgxcos+1=2cosx+tgx x∊<0,2π>
doszedłam do postaci (2cosx−1)(sinx−cosx)=0
II. tu mam problem, ponieważ podniosłam do kwadratu sinx−cosx=0 ==> sin2x=1 i z tego wyszlo mi
| | π | | 5 | |
x= |
| , a w odpowiedziach jest jeszcze x= |
| π |
| | 4 | | 4 | |
5 kwi 21:23
ICSP: | | π | |
sin2x = 1 ⇒ x = |
| + kπ dla k = 0 , 1 dostajemy takie x1 , x2 że x1,x2 ∊ [0 , 2π] |
| | 4 | |
5 kwi 21:28
Bershka: nic nie rozumiem z tego co napisałeś

5 kwi 21:31
ICSP: a jak rozwiązałeś/aś równanie sin2x = 1 ?
5 kwi 21:34
Bershka: | | π | | π | |
z wykresu, 2x= |
| wiec x= |
| |
| | 2 | | 4 | |
5 kwi 21:36
ICSP: a okresowość ?
5 kwi 21:37
Bershka: chyba, ze jest cos takiego ze wydluzam wykres do 4π i wtedy dopiero patrzę?
5 kwi 21:37
5-latek:
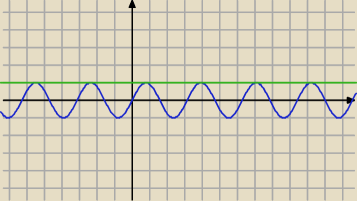
niebieski y=sin(2x)
zielony y=1
5 kwi 21:39
Bershka: ok juz wiem, dzieki

5 kwi 21:41
5 kwi 21:42
ICSP: Przejrzyj tamte przykłady
5 kwi 21:42

 niebieski y=sin(2x)
zielony y=1
niebieski y=sin(2x)
zielony y=1
