. Archy: Dany jest prostokąt ABCD, w którym AB:AD=√2. Punkt S jest środkiem boku AB. Oblicz miarę kąta między prostymi AC i DS.

Zenek:

a
	=√2⇔a=√2*b
b

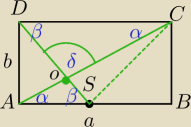
|AC|²=b²+(b√2)² |AC|=b√3 |SD|²=b²+(U{1}{b√2)²

	√6
|SD|=
	3

W ΔDAS:

	b
sinβ=
	|SD|

	√6
sinβ=
	3

	1
ΔAOS∼ΔDOC w skali k=
	2

|AO|=x |OC|=2x 3x=b√3

	2b√3
2x=
	3

Z tw sinusów w ΔDCO:

OC		a
	=		⇔
sinβ		sinδ

|OC|*sinδ=a*sinβ

2b√3		√6
	*sinδ=b√2*		⇔
3		3

2√3*sinδ=√12 sinδ=1 δ=90^o ======== sprawdź czy tyle w odpowiedzi.

Archy: nie mam odpowiedzi, ale wielkie dzięki za rozwiązanie

Utem:

Archy:

	√2b
W 4 linijce sie pomyliles. Ma byc		2
	2

Mila: Nie zapisana 2 w mianowniku, ma być :

	1
(		*b√2)2
	2

Archy: to miałem na myśli.

	1
Więc wyszło sinδ=
	6

Mila: Zaraz przeliczę wszystko .

Archy: pomyliłem się. Liczę jeszcze raz

Archy: nieno według mnie dobrze

Archy: czyli byłoby 10 stopni nie podoba mi sie ten wynik

Archy: mógłby ktoś zerknąć na to zadanko?

Mila:

	1
|AS|=		a
	2

a
	=√2⇔a=b√2
b

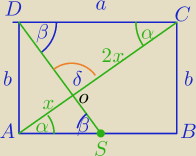
1) |AC|²=a²+b²⇔|AC|²=(b√2)²+b²=3b² |AC|=b√3

	1
|DS|2=b2+(		b√2)2
	2

	b2		3
|DS|2=b2+		=		b2
	2		2

	b√6
|DS|=
	2

W ΔDAS:

	b		b
sinβ=		=
	DS		b√6   2

	2		2√6
sinβ=		=
	√6		6

	√6
sinβ=
	3

============

	1
ΔAOS∼ΔDOC w skali k=
	2

|AO|=x |OC|=2x

	b√3
3x=b√3⇔x=
	3

	2b√3
|OC|=2x=
	3

|OC|		a
	=		⇔|OC|*sinδ=a*sinβ
sinβ		sinδ

2b√3		√6
	*sinδ=b√2*
3		3

2√3*sinδ=√12 2√3*sinδ=2√3 sinδ=1

	π
δ=
	2

=======

Mila: Teraz sprawdzaj.

Archy: ok dziękuję

Archy: Zenkowi itak wynik wyszedł dobry

Mila: Bo tam była tylko literówka.

Archy: no chyba że tak

Eta: Zenek= Mila