trygonometria, szereg mikejjla: Rozwiąż nierówność: sin²x+sin³x+sin⁴x+...≥¹₂ dla ∊(0;π) Cały czas wychodzi mi zły wynik, mógłby ktoś to rozwiązać? Tą lewą stronę chyba trzeba rozwiązać z szeregu geometrycznego.

Ann: ile powinno wyjść?

Ann:

sin2x		sin2x−0,5(1−sinx)
	−0,5=
1−sinx		1−sinx

sinx=t

t2+t−0,5		3   (t−1)2+3t−   2		3		5
	=		=−t+1−3t+		=−4t+		≥0
1−t		−(t−1)		2		2

dalej już spokojnie dasz sobie radę

	5
Czy powinno wyjśc sinα<=		?
	8

mikejjla:

	π		π		π		5π
x∊<		;		)∪(		;		>
	6		2		2		6

Ann: :<

mikejjla: no niestety

mikejjla: ja robiłam tak: |q|<1 |sinx|<1 sinx<1 ⋀ sinx>−1 sinx∊(−1;1)

sin2x		1
	−		≥0
1−sinx		2

sin2x −1 + sinx
	≥0
2(1−sinx)

−2(sinx−1)(sin²x+sinx−1)≥0 (sinx−1)(sin²x+sinx−1)≤0 sinx=1 a z tego równania kwadratowego to jakieś dziwy niesłychane wychodzą

Mila:

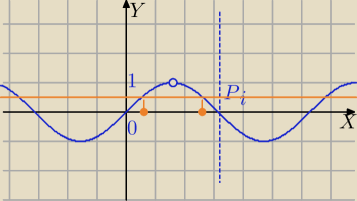
	π		π
|sinx|<1 i x∊(0;π)⇔x∊(0,		)∪(		,π)
	2		2

sin2x		1
	≥		/*2
1−sinx		2

2sin2x		2sin2x
	≥1⇔		−1≥0
1−sinx		1−sinx

2sin2x−1+sinx
	≥0 i x∊D⇔
1−sinx

(2sin²x+sinx−1)*(1−sinx)≥0 1) 1−sinx≤0 i (2sin²x+sinx−1)≤0 i x∊D Pierwsza nierówność sprzeczna lub 1−sinx≥0 i (2sin²x+sinx−1)≥0 i x∊D, sinx=t,

	−1−3		−1+3		1
spełniona dla x∊D i Δ=9⇔t=		=−1 lub t=		=		⇔
	4		4		2

	1
t≤−1 lub t≥
	2

sinx≤−1 brak rozwiązań

	1		π		π		π		5π
lub sin x≥		i x∊D⇔x∊<		,		)∪(		,		>
	2		6		2		2		6

mikejjla: dziękuję <3

Mila: