zadania
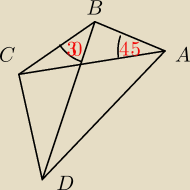
Blue: Przekątna AC czworokąta ABCD ma długość √5 i tworzy z bokiem AB kąt o mierze 45
0. Przekątna
BD ma długość 5√3 i tworzy z bokiem BC kąt o mierze 30
0. Oblicz długość boku CD wiedząc, że
bok AB ma długość 2√10 .
Wszystko ładnie pięknie, ale mi wychodzi z dwóch tw. cosinusów 5, a odpowiedź mam inną....
Czy ja coś źle liczę

Ile Wam wyszło?

5 kwi 14:42
kyrtap:
|AC| =
√5
|BD| = 5
√3
|AB| = 2
√10
Z tw cosinusów dla Δ CAB
|BC|
2 = |AC|
2 + |AB|
2 − 2|AC||AB| cos45
| | √2 | |
|BC|2 = 5 + 40 − 2√5 2√10 |
| |
| | 2 | |
|BC|
2 = 45 − 25 = 25 ⇒ |BC| = 5 (bo |BC|>0)
Z tw. cosinusów dla Δ CBD
|CD|
2 = |CB|
2 + |BD|
2 − 2|CB||BD|cos30
| | √3 | |
|CD|2 = 25 + 75 − 2 *5*5√3 |
| |
| | 2 | |
|CD|
2 = 100 − 75 = 25 ⇒ |CD| = 5 (bo |CD|>0)
5 kwi 14:56
kyrtap: też mi tak wyszło ^^
5 kwi 14:56
kyrtap: w odpowiedziach jaki jest wynik?
5 kwi 14:58
Blue: 3
√2
Chyba coś jest źle w tych odp. najwyraźniej

5 kwi 15:49
Kacper:

6 kwi 19:02
 Ile Wam wyszło?
Ile Wam wyszło?
 |AC| = √5
|BD| = 5√3
|AB| = 2√10
Z tw cosinusów dla Δ CAB
|BC|2 = |AC|2 + |AB|2 − 2|AC||AB| cos45
|AC| = √5
|BD| = 5√3
|AB| = 2√10
Z tw cosinusów dla Δ CAB
|BC|2 = |AC|2 + |AB|2 − 2|AC||AB| cos45
 Chyba coś jest źle w tych odp. najwyraźniej
Chyba coś jest źle w tych odp. najwyraźniej 
