Geometria płaska ela_pik31: W okrąg o promieniu r=√10 wpisano trapez abcd, w którym AB równoległe do DC. Wiedząc, że długość odcinka BD wynosi 6 oraz długość AD wynosi 4√2, oblicz pole tego trapezu.

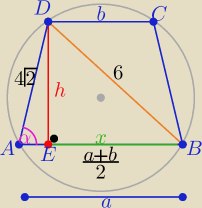
Eta: 1/ z tw. sinusów w trójkącie ABD

6		3√10
	=2R ⇒ sinα=
sinα		10

to h=4√2*sinα ⇒ h= ............

	a+b
|EB|=x=		to x=√62−h2=......
	2

P(trapezu)= ...........

Kobe: Trochę odświeżam. Dlaczego x=(a+b)/2 ?

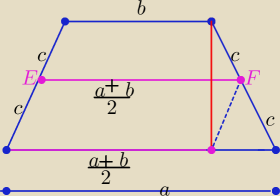
Eta: |EF|−−− dł. środkowej trapezu

	a+b
|EF|=
	2

Kobe: O kurcze. Wyleciało mi to, że trapez wpisany w okrąg musi być równoramienny, dziękuje bardzo za pomoc