zadania Blue:

	1
zad.1 Ile rozwiązań ma równanie sinx=		w przedziale (−570o, 570o) ?
	3

zad.2 Wyznacz wszystkie wartości parametru m, dla którego równanie 2015^2x−6*2015^x +m²−8m = 0 ma dokładnie jedno rozwiązanie.

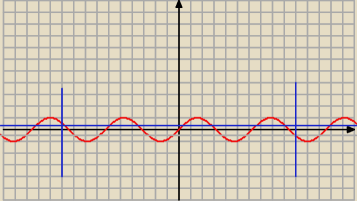
Janek191: z.1

Janek191: z.2 t = 2015^x t² − 6 t + m² − 8 m = 0 Δ = 36 − 4 m² + 32 m = 0 ( m − 9)*( m + 1) = 0 m = − 1 lub m = 9 ===============

Blue: Janek, ale czy odpowiedź do tego 1 nie powinna być 6 Bo tak mi się wydawało, ale w odpowiedziach mam 7 ...

Blue:

	1		1
Dobra, już widzę sin−570= sin30, więc będzie tam		, czyli wykres przetnie		,
	2		3

zgadza się

Blue: Janek, w tym drugim odpowiedź jest m∊<0,8>U{−1,9}.W odpowiedziach mam tylko napisane, że należy rozpatrzyć przypadki: a) Δ>0 i t₁*t₂<0 b) Δ=0 t₀>0 c) Δ>0 t₁=0 t₂>0 Wyjaśni to ktoś

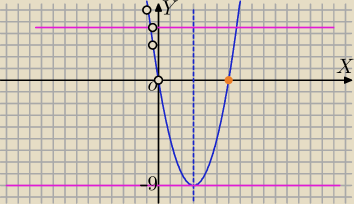
Utem: 2015^2x−6*2015^x=−m²+8m f(x)=2015^2x−6*2015^x 2015^x=t,t>0 f(t)=t²−6t t_w=3 y_w=3²−6*3=−9 Jedno rozwiązanie dla : 1) −m²+8m=−9 m²−8m−9=0 Δ=64+4*9=100

	8−10
m=		=−1 lub m=9
	2

================== 2) −m²+8m≥0 przecięcie z prawym ramieniem paraboli m²−8m≤0 m*(m−8)≤0⇔ m∊<0,8> ============= dokończ.

Mila: Tam powinna być opisana oś pozioma jako t, a z założenia t>0 więc części wykresu po lewej stronie osi OY nie bierzemy pod uwagę.

Blue: Ok, Mila, a wyjaśnisz to rozwiązanie, które podali w odpowiedziach Bardzo proszę

Kacper:

Mila: Masz podstawienie : 2015^x=t Funkcja y=2015^x jest funkcją różnowartościową i przyjmuje wartości dodatnie, więc musisz te warunki uwzględnić w rozwiązaniu równania: t²−6t+m² − 8 m =0 Masz mieć jedno rozwiązanie dodatnie i są warunki rozpisane: jedno ujemne, jedno dodatnie dokładnie jedno dodatnie jedno zero , jedno dodatnie Zalecam jednak graficzne rozwiązanie , przy czym pamiętać, że t>0 i tylko część wykresu brać pod uwagę.

Blue: ok, dziękuję bardzo