w kulę o promieniu R wpisano stożek
Stupid: W kulę o promieniu R wpisano stożek, którego tworząca jest nachylona do płaszczyzny podstawy
pod kątem α . Oblicz pole powierzchni całkowitej Pc i objętość V.
Proszę o pomoc
4 kwi 19:36
Eta:
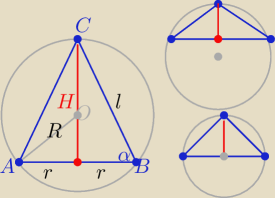
W zależności od miary kąta α ( trzy przypadki wpisania stożka w kulę patrz rys.
l −−− dł tworzącej stożka
| | l | |
Z tw. sinusów w trójkącie ABC: |
| =2R ⇒ l=2R*sinα |
| | sinα | |
| | r | |
i |
| = cosα ⇒ r= l*cosα = 2Rsinα*cosα= Rsin(2α) |
| | l | |
H= r*tgα= 2Rsin
2α
V=............
P
c=..........
4 kwi 20:01
Stupid: Dzięki ci wielkie Eta

Czy znalazłabyś czas na jeszcze 1 zadanko?
5 kwi 13:01
Frost: Daj zrobię

nudno dziś

5 kwi 13:03
Stupid: W kulę o promieniu 6cm wpisano ostrosłup prawidłowy trójkątny o największej objętości. Wykaż,
że ostrosłup ten jest czworościanem foremnym, którego krawędź ma długość 4 √6.
5 kwi 13:33
Eta:
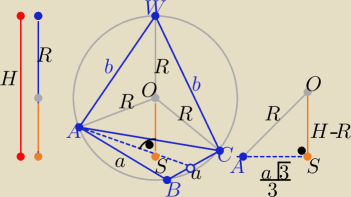
| | a√3 | |
R=6 , |AS|= |
| |SW|=H −−ostrosłupa , to |OS|=H−R |
| | 3 | |
Z tw. Pitagorasa w trójkącie ASO
| | a2 | | a2 | |
62=(H−6)2+ |
| ⇒ |
| = 12H−H2 |
| | 3 | | 3 | |
| | √3 | | √3 | |
V(H)= |
| *H(12H−H2) = |
| (12H2−H3) |
| | 4 | | 4 | |
V
'(H)=0 ⇒ 24H−3H
2=0 ⇒ H
2−8H=0 ⇒ H=8
to a
2=3(96−64) ⇒ a= 4
√6 i H=8 to b=
√64+32= 4
√6
zatem takim ostrosłupem jest czworościan o krawędzi
a=4√6
c.n.w.
5 kwi 15:46
Stupid: Mam coś jeszcze xd
W stożek wpisano walec w ten sposób, że dolna podstawa walca zawiera się w podstawie stożka,
a okrąg górnej podstawy walca zawiera się w powierzchni bocznej stożka. Kąt rozwarcia stożka
jest PROSTY. Pole powierzchni całkowitej walce jest równe polu powierzchni bocznej stożka.
Wykaż, że odległość stożka od górnej podstawy walca jest równa połowie długości tworzącej
stożka.
5 kwi 15:56
Eta:
Teraz wychodzę

będę dopiero ok 20
oo
5 kwi 15:58
 W zależności od miary kąta α ( trzy przypadki wpisania stożka w kulę patrz rys.
l −−− dł tworzącej stożka
W zależności od miary kąta α ( trzy przypadki wpisania stożka w kulę patrz rys.
l −−− dł tworzącej stożka
 Czy znalazłabyś czas na jeszcze 1 zadanko?
Czy znalazłabyś czas na jeszcze 1 zadanko?
 nudno dziś
nudno dziś 

 będę dopiero ok 20oo
będę dopiero ok 20oo