zadania optymalizacyjne masterofkapcie: Dany jest wykres funkcji y=x², dla x≥0. Prosta l styczna do tego wykresu wraz z prostymi x=0, y=4, y=0 wyznacza trapez. Oblicz współrzędne takiego punktu styczności, by ten trapez miał najmniejsze pole.

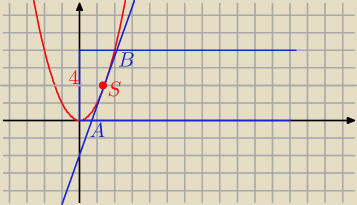
Janek191: y = x² y = a x + b −−−−−−−−−− x² = a x + b x² − a x − b = 0 Δ = a² − 4*1*(−b) = a² + 4 b = 0 ⇒ 4 b = − a² ⇒ b = − 0,25 a² y = a x − 0,25 a² −−−−−−−−−−−−−−−−−−−−−− 1) y = 0 0 = a x − 0,25 a² a x = 0,25 a² x = 0,25 a −−−−−−−−−−−−−−−− A = ( 0,25 a , 0) ============== 2) y = 4 4 = a x − 0,25 a² a x = 4 + 0,25 a²

	4
x =		+ 0,25 a
	a

	4
B = (		+ 0,25 a, 4)
	a

================== Pole trapezu:

	4		4		8
P = 0,5*(		+ 0,25 a + 0,25 a)*4 = 2*(		+ 0,5 a) =		+ a
	a		a		a

P(a) = U{8}[a} + a

	8
P' (a) = −		+ 1 = 0 ⇔ a = 2√2
	a2

P''(a) = U{16}[a³} więc

	16
P ''( 2√2) =		= U{1}[√2} = U[√2}{2} > 0
	16√2

Funkcja P osiąga minimum dla a = 2√2 Prosta styczna ma postać y = 2√2 x + b₁ i przechodzi przez punkt A = ( 0,25 a , 0) = 0,5 √2 , 0) 0 = 2√2*0,5√2 + b₁ 0 = 2 +b₁ b₁ = − 2 y = 2√2 x − 2 x² = 2√2 x − 2 x² − 2√2 x + 2 = 0 Δ = 0

	2√2
xo =		= √2
	2

y_o = 2√2*√2 − 2 = 2 S = ( x_o , y_o) = ( √2, 2) ====================