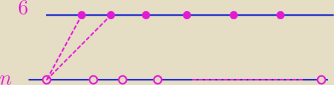
Prawdopodobieńśtwo Tripper: Na płaszczyźnie dane są dwie proste równoległe niepokrywające się. Na jednej z nich zaznaczono sześć punktów, a na drugiej − n punktów, gdzie n ≥ 2. Oblicz n, jeśli prawdopodobieństwo tego, że trzy losowo wybrane punkty spośród zaznaczonych są wierzchołkami trójkąta, jest równe

	9
	14

Mila:

	6 2		n 2
|A|=		*n+		*6− liczba wybranych punktów, które mogą byc wierzchołkami Δ.

	n+6 3
|Ω|=

	6 2   n 2   *n+ *6
P(A)=
	1   *(n+6)*(n+5)*(n+4) 6

	9
P(A)=
	14

Dokończ