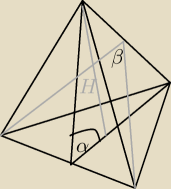
` czoko: W ostrosłupie prawidłowym trójkątnym kąt między ścianą boczną a podstawą jest równy α. Oblicz cosinus kąta między ścianami bocznymi tego ostrosłupa. nie wiem jak się do tego zabrać :C

	a√3   6
jedyne co wpadło mi do głowy to to, że cosα=
	H

czoko:

czoko: nikt nic?

Martiminiano: Mam pomysł, zaraz napiszę

czoko: ok super

Martiminiano: Spróbuję to opisać, bo z rysowaniem u mnie szału nie ma Najpierw oznaczę jakoś ten ostrosłup. Niech będzie w podstawie od lewej strony ABC i wierzchołek S. Spodek wysokości T i punkt boku AB oznaczę M.

	a√3
Więc najpierw w trójkącie MTS wyznaczam, że H= tgα
	6

Teraz w trójkącie TCS wyznaczam długość krawędzi bocznej.

	√a2(tg2α+4)
I wynosi ona
	√12

Martiminiano: Zdałem sobie teraz sprawę, że moje rozwiązanie jest zbyt skomplikowane... Na pewno musi być jakieś prostsze. Dążyłem do wyznaczenia ramienia tego trójkąta równoramiennego, w którym jest kąt β.