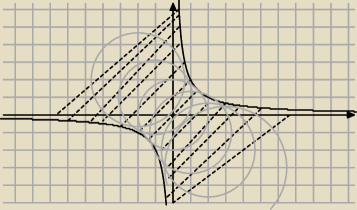
rodzina kół YushokU: Witam, Mam kłopot z ocenieniem pewnego zadania Nierównośc (x−a)²+(y+a)²≤a²+4 opisuje pewną rodzinę kół. Zaznacz w układzie współrzędnych wszystkie punkty (x,y) , które należą do tej rodziny.

	2
Metodą rysowania kółek w układzie zauważyłem, że wyznaczają one hiperbolę		, co
	x

zaznaczyłem w komentarzu do zadania. Następnie zgodnie z poleceniem zaznaczyłem te punkty pisząc że zaznaczam punkty spełniające równanie xy≤2 No i patrząc do odpowiedzi mam jakieś kosmiczne obliczenia z których to wynika, i sie zastanawiam, czy skoro w poleceniu było zaznacz to mogę tak załatwić sprawę? Wiem, że większość osób, które tu siedzi to uczniowie albo studenci, ale jak ktoś ma jakieś pojęcie na ten temat, to proszę o odpowiedź

PW:

	2
Metodą rysowania kółek w układzie zauważyłem, że wyznaczają one hiperbolę		.
	x

Jak na to wpadłeś bez tych "kosmicznych obliczeń"?

YushokU: Dla a=1 okrąg zawiera punkt (2,1) i (−1,−2) A dla a=−1 okrąg zawiera punkty (1,2) i (−2,−1) A rysując kilka kół w układzie współrzędnych widać, że ma to jakąś regularność. Wiem, że to wszystko jest mało profesjonalne, ale mimo wszystko mam nadzieję, że jakieś punkty byłyby za to przyznane

PW: 1 punkt za genialną intuicję.

Bogdan: x − a)² + (y + a)² ≤ a² + 4 x² − 2ax + a² + y² + 2ay + a² − a² − 4 ≤ 0 a² − 2(x − y)a + x² + y² − 4 ≤ 0 Założenie: Δ ≥ 0 Δ = 4(x² − 2xy + y²) − 4(x² + y² − 4) ≥ 0 ⇒ 2xy ≤ 4 ⇒ xy ≤ 2

	2
dla x < 0: y ≥
	x

	2
dla x > 0: y ≤
	x

YushokU: Dziękuję za to rozwiązanie Ja nawet nie pomyślałem, żeby tu coś obliczać, liczyłem, że to zadanie chce abym coś zauważył, tak to może zacząłbym coś kombinować