Trójkąt równoboczny Nata: Proszę o pomoc: Punkt D (−2,−1) jest spodkiem wysokości opuszczonej z wierzchołka A (4,2) trójkąta równobocznego ABC. Wyznacz współrzędne środka okręgu opisanego na tym trójkącie oraz współrzędne pozostałych wierzchołków tego trójkąta.

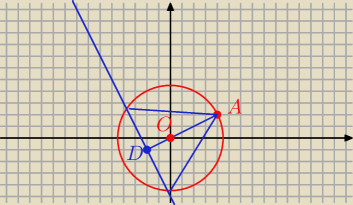
Janek191: Mamy Prosta AD y = a x + b 2 = 4a + b − 1 = − 2 a + b −−−−−−−−−−− odejmujemy stronami 3 = 6 a a = 0,5 b = 2 a − 1 = 0 y = 0,5 x ========= Prosta prostopadła do pr AD , czyli prosta BC przechodząca przez D y = − 2 x + b₁ − 1 = −2*(−2) + b₁ − 1 = 4 + b₁ b₁ = − 5 y = − 2 x − 5 ========= oraz O = ( x, y) → →

	1
DO =		DA
	3

	1
[ x − (−2) , y −(−1) ] =		[ 6, 3 ]
	3

[ x + 2 , y + 1] = [ 2 , 1} więc x = 0 i y = 0 O = ( 0,0) − środek okręgu opisanego

Janek191: r² = I OA I² = ( 4 −0)² + ( 2 −0)² = 20 Równanie okręgu x² + y² = 20 y = − 2 x − 5 ⇒ y² = 4 x² + 20 x + 25 −−−−−−−−− x² + 4 x² + 20 x + 25 = 20 5 x² + 20 x + 5 = 0 / : 5 x² + 4 x + 1 = 0 Δ = 16 − 4*1*1 = 12 = 4*3 √Δ = 2√3

	− 4 − 2√3
x =		= − 2 − √3 lub x = −2 + √3
	2

więc y = −2*( −2 −√3) − 5 = 4 + 2√3 − 5 = 2√3 − 1 lub y = −2*( − 2 +√3) − 5 = 4 − 2√3 − 5 = − 2√3 − 1 B = ( − 2 − √3 , 2√3 − 1) C = ( − 2 + √3, − 2√3 − 1) ===============================================

Nata: Dziękuję bardzo!