Stereometria i równanie trygonometryczne, proszę o pomoc :) Arek: 1) Podstawą ostrosłupa ABCS jest trójkąt równoramienny ABC , w którym |AB | = 6, |BC | = |AC | = 10 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 60 stopni. Oblicz objętość tego ostrosłupa. 2) Rozwiąż równanie cosx + sin 3x = 0 .

J:

	3
2) ⇔ sin3x = −cosx ⇔ sin3x = sin(		π + x)
	2

Arek: Czy można przekształcić cosinus na sinus dzięki 1 trygonometrycznej, a po przekształceniu skorzystać ze wzoru na sumę sinusów?

J: można, tylko po co ? naprawdę chcesz sobie utrudniać życie ?

Arek: Bo na pierwszy rzut oka nie wpadłbym na Twoje rozwiązanie, dziękuję

Arek: Wie może ktoś jak rozwiązać pierwsze zadanie? Tyle wiem że skoro krawędzie nachylone są pod tym samym kątem to spodek wysokość pada na środek okręgu wpisanego w podstawę

dero2005: Jeśli wszystkie krawędzie boczne są pochylone pod jednakowym kątem do podstawy to spodek wysokości leży w środku okręgu opisanego na podstawie, oblicz pole podstawy a potem ze wzoru

	a*b*c
R =		oblicz promień okręgu, następnie oblicz wysokość ze wzoru H = Rtg60o
	4S

Arek:

	50
Pole podstawy ze wzoru herona wychodzi mi 3√91 promień R=		a wysokość to już w
	√91

	50√273
ogóle paskudny zapis:		, czy zrobiłem gdzieś błąd? z góry dziękuję za pomoc
	91

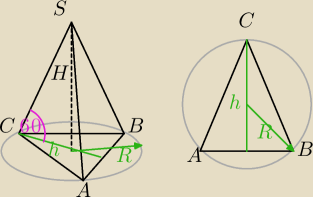
dero2005: AB = a = 6 AC = BC = b = 10 h = √b² − (^a₂)² = √10²−3² = √91

	a*h
S =		= 3√91
	2

	ab2		50√91
R =		=
	4S		91

H
	= tg60o = √3
R

	R		50√273
H =		=
	√3		273

	S*H		50
V =		=		√24843
	3		273

wyniki są obrzydliwe

Arek: Dziękuję za pomoc, nie zawsze to co brzydko wygląda jest złe