Funkcja liniowa Pieseł: Wyznacz wzór funkcji liniowej f, jeśli f(1) = 3, a wartości ujemne funkcja przyjmuje tylko dla argumentów mniejszych od −3.

Qulka: y=3(x−1)/4+3

Pieseł: Uszanowanko.

Pieseł: A jak do tego doszłaś?

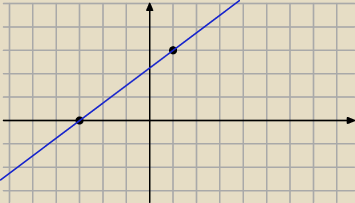
J: funkcja ma postać: y = ax + b f(1) = 3 , zatem: 3 = a*1 + b f(−3) =0 , zatem: 0 = a(−3) + b

	3		9
z tego układu równań dostajemy: a =		i b =
	4		4

	3		9
szukana prosta: y =		x +
	4		4

Mikołaj: Do wyznaczenia funkcji liniowej potrzebujemy co najmniej dwóch punktów. z treści zadania: f(1) = 3 czyli dla x=1 => y=3 a wartości ujemne czyli y<0 są przyjmowane dla x<−3, więc pojawia się tutaj punkt charakterystyczny (miejsce zerowe funkcji) => y=0 to x=−3 Tworzymy układ równań: Wzór ogólny funkcji liniowej to y=ax+b, więc: a,b współczynniki których szukamy. {0=−3a+b {3=a+b ten układ równań rozwiązujesz a=3/4 b=9/4 podstawiam do wzoru funkcji: y=(3/4)x + 9/4 czyli łatwiej f(x)=0,75x+2,25

Pieseł: Uszanowanko bardzo!