rachu
bezendu:
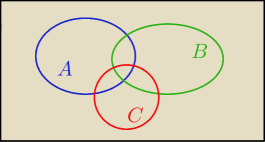
Podaj wzór na P(A∪B∪C)
P(A∪B∪C)=P(A∪B)+P(C)−P(A∩B∩C)−P(A∩C)−P(C∩B) ?
2 kwi 22:06
Qulka: P(A∪B∪C)=P(A)+P(B)+P(C)+2P(A∩B∩C)−P(A∩C)−P(C∩B)−P(A∩B)
2 kwi 22:15
bezendu:
Dla dwóch zbiorów nie mam problemu, ale jaki algorytm jest dla n>2 zbiorów ?
2 kwi 22:25
Qulka: nie wiem
liczyłam na piechotę
2 kwi 22:27
bezendu:
Ok, dziękuję.
2 kwi 22:31
bezendu:
Qulka zarzuć jakiś przykładem do samodzielnego zrobienia ?
Na 3 zbiorach
2 kwi 22:44
Qulka: przykładem czego?
2 kwi 22:47
bezendu:
Chodzi mi o działania na zbiorach (diagramy Venna) patrz przykład 22:06
2 kwi 22:49
Qulka: wszystkie zadania z 3 robi się po prostu na piechotę
2 kwi 22:49
Mila:
Łączność:
P(A∪B∪C)=P([A∪B]∪C)=
=P(A∪B)+P(C)−P([A∪B]∩C)=
=P(A)+P(B)−P(A∩B)−P((A∩C)∪(B∩C))=
=P(A)+P(B)−P(A∩B)−[P(A∩C)+P(B∩C)−P(A∩C∩B∩C)]=
=P(A)+P(B)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)]
Zrób to:
P(A∪B∪C∪D)
2 kwi 22:50
Qulka: jak znajdę ten temat co ma 3600 postów to w nich jest fajne zadanko
ale to chwilę potrwa
2 kwi 22:50
bezendu:
P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)+3(PA∩B∩C∩D)−P(A∩B)−P(A∩B)−P(A∩C)−P(A∩D) ?
2 kwi 22:56
2 kwi 23:08
bezendu:
Dziękuję, już biorę się za liczenie.
2 kwi 23:08
bezendu:
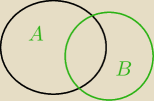
A∪(A∩B)=A
Wystarczy rysunek ?
P(A)=P(A\B)+P(A∩B) ?
2 kwi 23:14
Qulka: a chcesz ćwiczyć rysunki czy wypisywanie dowodów ?
2 kwi 23:45
bezendu:
Raczej dowód, w technikum uczyłem się na rysunkach, ale to polegało raczej na policzeniu P(..)
2 kwi 23:47
2 kwi 23:52
2 kwi 23:53
bezendu:
To może jednak będę rysował
2 kwi 23:54
msp: mam pytanie jaki to jest poziom?
2 kwi 23:55
Qulka: jak dla mnie poziom 1 klasy technikum
wówczas się tego uczyłam
ale teraz to chyba
pomaturalny
2 kwi 23:59
msp: też mi się tak wydaje
3 kwi 00:00
Qulka: ale i logika i zbiory są w LO i chyba nawet zaraz na początku
więc bez zmian
3 kwi 00:04
Qulka: do samego zapisu nieco trzeba dojrzeć..ale tabelkę może robić
3 kwi 00:04
msp: akurat teraz prawdopodobieństwo i kombinatoryka są na samiutkim końcu wg podręczników i masa
nauczycieli nawet nie zdąży zacząć tego przed maturą
3 kwi 00:06
bezendu:
Logikę miałem w pierwszym semestrze, kwantyfikatory też rozumiem.
3 kwi 00:06
Qulka: zdążyłam zapomnieć że to miało być prawdopodobieństwo na zbiorach
3 kwi 00:11
3 kwi 00:12
bezendu:
Własnie raczej zadania z tego pierwszego linku bardziej
3 kwi 00:15
Qulka: oki
jak wolisz
3 kwi 00:20
bezendu:
Dowód C bardzo mi się podoba, wszystko tam rozumiem, tylko czemu sprawdzamy pary uporządkowane
i nie ?
3 kwi 00:28
Qulka: bo to akurat przykład z iloczynem kartezjańskim a tam są pary uporządkowane
3 kwi 00:29
bezendu:
Możesz spojrzeć na ten rysunek 23:14 ?
3 kwi 00:31
Qulka: rysunek trzeba by zakreskować jeśli miałby być dowodem
3 kwi 00:33
bezendu:
I takie coś było by zaliczone ?
3 kwi 00:39
Qulka: po odpowiednim zakreskowaniu tak
3 kwi 00:40
bezendu:
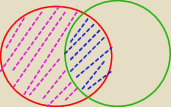
Dziękuję
P(A\B)+P(A∩B)=P(A) ?
3 kwi 00:44
Qulka: tak
3 kwi 00:49
Mila:
P(A∪B∪C∪D) masz źle, trzeba pracowicie rozpisywać.
To trochę żmudne, ale możliwe do wykonania.
3 kwi 18:45
bezendu:
Zaraz spróbuję poprawić.
3 kwi 19:53
bezendu:
Jakoś nie mogę wpaść na poprawne rozwiązanie ?
3 kwi 22:52
Mila:
Korzystamy z równości:
|AUBUC|=|A|+|B|+|C|−|A∩B|−|A∩C|−|B∩C|+|A∩B∩C|
|AUBUCUD|=|(AUBUC)UD)|=
=|(AUBUC)|+|D|−|(AUBUC)∩D|=
=|A|+|B|+|C|−|A∩B|−|A∩C|−|B∩C|+|A∩B∩C|+|D|−|(A∩D)U(B∩D)U(C∩D)|=
=|A|+|B|+|C|−|A∩B|−|A∩C|−|B∩C|+|A∩B∩C|+|D|−{|(A∩D)|+|(B∩D)|+
+|(C∩D)|−|A∩B∩D|−|A∩C∩D|−|(B∩C∩D)|+|A∩B∩C∩D|}=
=|A|+|B|+|C|+|D|−|A∩B|−|A∩C|−|B∩C|−|(A∩D)|−|(B∩D)|−|(C∩D)|+|A∩B∩C|+
+|A∩B∩D|+|A∩C∩D|+|(B∩C∩D)|−|A∩B∩C∩D|
3 kwi 23:04
bezendu:
Dziękuję. Spróbuje analizować.
3 kwi 23:11
Mila:
3 kwi 23:31
bezendu:
Ale i tak nadal to trudne dla mnie
3 kwi 23:47
bezendu:
Już zrozumiałem !
4 kwi 23:36
Mila:
Wiedziałam, że tak będzie.
4 kwi 23:40
bezendu:
Jeszcze sobie poćwiczę dowody od Qulki
4 kwi 23:41
