optymalizacyjne margaret: drut o długości 72 cm rozcięto na dwa kawałki i z każdego zbudowano brzeg trójkąta równoramiennego przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi 5:8 a w drugim 13:10. Jakie obwody mają te trójkąty jeżeli suma ich pól jest najwieksza z możliwych?

margaret: pomoze ktos?

Eta: http://www.zadania.info/d1/6009387

margaret: w drugiej linijce wyliczeń f(b) nie ma blędu? wedlug mnie powinno byc

	12		100		60		12		10		12
=(		*		+		)b2−2*		*20*		b+202*
	25		169		169		25		13		25

margaret: zle wtedy nie wychodzi prawidlowa odpowiedz...

margaret: pomoze mi ktos?

margaret: ....

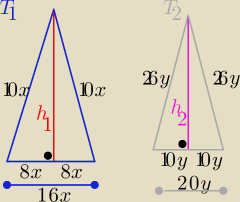
Eta: W zadaniu powinnaś napisać " suma pól najmniejsza z możliwych" Wprowadzam bardziej przyjazne obliczeniom ( oznaczenia) jak na rys. x, y>0 h₁=√100x²−64x²=6x i h₂=√676y²−100y²= 24y P₁= 48x² P₂= 240y² L₁+L₂= 72 ⇒ 36x+72y=72 ⇒ x+2y=2 ⇒ x= 2−2y , y∊(0,1) F=P₁+P₂ = 48x²+240y² F(y)= 48*4(1−y)²+240y² = 432y²−384y+192 dokończ .........

Eta: No i co? Ja poświęcam swój czas a margaret ......... poszła sobie (echhh