| 1 | ||
długości boków czworokąta opisanego na czworokącie wcześniej powstałym stanowi | Pola | |
| 2 |

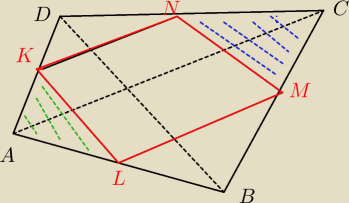 KL to odcinek łączący środki boków AB i AD w trójkącie ABD, więc KL jest połową BD i jest
równoległy do BD.
KL to odcinek łączący środki boków AB i AD w trójkącie ABD, więc KL jest połową BD i jest
równoległy do BD.
| 1 | ||
Trójkąt AKL jest podobny do trójkąta ABD w skali k= | , więc | |
| 2 |
| 1 | ||
pole trójkąta AKL to | pola trójkąta ABD | |
| 4 |
| 1 | ||
PAKL= | PABD | |
| 4 |
| 1 | 1 | |||
Trójkąt MCN jest podobny do trójkąta BCD w skali k= | , więc pole trójkąta MCN to | |||
| 2 | 4 |
| 1 | 1 | 1 | 1 | |||||
PAKL+P{MCN}= | PABD+ | PBCD= | (PABD+PBCD)= | PABCD | ||||
| 4 | 4 | 4 | 4 |
| 1 | ||
PDKN+PLBM= | PABCD, a stąd: | |
| 4 |
| 1 | ||
PAKL+PBLM+PMCN+PDKN= | PABCD, czyli | |
| 2 |
| 1 | ||
PKLMN= | PABCD | |
| 2 |
