nierówność hehes: Witam mam pytanko o to zadanie Znajdz wszystkie liczby naturalne spełniające nierówność 4 − x > √ x² + x − 2 wyznaczam dziedzine x²+x − 2 >= 0 i wychodzi x1 = −2 i x2= 1 czyli dziedziną są liczby rzeczywiste za wyłączeniem −2 i 1 ?

hehes: ?

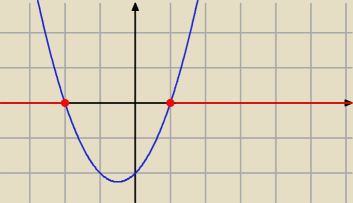
Qulka: dziedziną jest czerwony przedział czyli x∊(−∞;−2>u<1;+∞)

5-latek: Bzdury Podstawa za x=0 pod pierwiastek

PW: Ma być x² + x − 2 ≥ 0 (bo stoi pod pierwiastkiem), a więc nie tak.

hehes: o co chodzi bo się pogubiłem Czy to co napisała Qulka jest źle ?

hehes: Dobrze teraz dalsza część ... Podniosłem do kwadratu to równanie i wyszło mi x < 2 Jak mam to teraz zinterpretowac ? W odpowiedziach jest x=1 i nie wiem czy to błąd w odpowiedizach,czy ja czegoś nie rozumiem

PW: Skoro Qulka była szybsza, to muszę zwrócić uwagę na błąd w jej wypowiedzi: to czerwone nie jest przedziałem, to tylko suma dwóch przedziałów.

5-latek: Chodzi o twój post 22:24 Qulka Pozdrawiam napisala dobrze

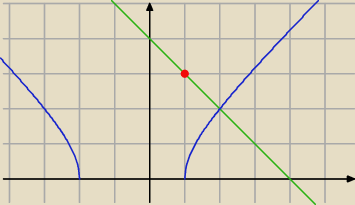
Qulka: rozwiązaniem całości to x=1

PW: Odpowiedź na pytanie z 22:39. Podnoszenie do kwadratu to operacja ryzykowna, jeśli nie wiemy że obie strony są dodatnie (nieujemne). Należało ograniczyć poszukiwania rozwiązań do takich x, dla których lewa strona jest nieujemna (bo jak jest ujemna, to na pewno nierówność zamienia się w zdanie fałszywe).

Qulka: ponieważ w zadaniu masz w zbiorze liczb NATURALNYCH

Jacek: A czy z samej nierówności w treści zadania nie powinno wynikać dla dziedziny 4−x>0, a więc dodatkowy warunek x<4?

hehes: PW mógłbys to jeszcze raz wytłumaczyć jakoś,albo o jakim sposobie rozwiązania mówisz ponieważ nie rozumiem tego

hehes: :( ?

hehes: góra prosiłbym o pomoc

Qulka: chciałeś podnieść nierówność obustronnie do kwadratu (o 22:39) a to niezdrowe

Qulka: poza tym wyszło ci x<2 i skoro to mają być liczby naturalne to jedyną jest x=1

hehes: to jaki jest sposób aby zrobic to dobrze,bez szalenstw ?

PW: Najpierw o podnoszeniu do kwadratu. Nie wolno podnosić stronami do kwadratu nierówności. Przykład: −7 > x² (ta nierówność nie ma rozwiązań, nie ma co się wysilać), a po podniesieniu stronami do kwadratu 49 > x⁴ (ta nierówność ma rozwiązania, łatwo zgadnąć np. x = 0, x = 1...). Dopiero gdy wiemy, że obie strony są nieujemne, podniesienie stronami do kwadratu daje nierówność równoważną (bo funkcja kwadratowa z² jest dla dodatnich argumentów rosnąca, a więc z₁ < z₂ ⇔ z₁² < z₂² dla nieujemnych z₁, z₂). Teraz o rozwiązaniu: Qulka prawidłowo wyznaczyła dziedzinę nierówności − sumę przedziałów (−∞;−2>∪<1;+∞). Widzimy (to już jest rozumowanie "jak to rozwiązać"), że dla x takich, że 4−x < 0 rozwiązań nie ma (bo lewa strona jest ujemnia, a prawa nieujemna). Nie ma więc czego szukać dla x > 4, ograniczamy poszukiwania rozwiązań do zbioru x∊(−∞, 4>. Dla takich x mamy nierówność o obu stronach nieujemnych, a więc po podniesieniu stronami do kwadratu otrzymamy równoważną określoną na części wspólnej dziedziny i zbioru (−∞, 4>, czyli na zbiorze (−∞;−2>∪<1, 4> (4 − x)² > x² + x −2, x∊(−∞;−2>∪<1, 4> 16 − 8x + x² > x² + x −2, x∊(−∞;−2>∪<1, 4> 18 > 9x, x∊(−∞;−2>∪<1, 4> x < 2, x∊(−∞;−2>∪<1, 4>. Liczba naturalna spełniająca tę nierówność jest tylko jedna: x = 1 (i ona jest rozwiązaniem zadania).

Jacek: No dobrze, ale czy 4−x>0, co ma związek z pierwiastkiem kwadratowym, nie jest warunkiem ograniczającym dziedzinę. Czy jakbym tak napisał to jest błąd?

hehes: Dziękuje bardzo za pomoc wszystkim,życze dobrej nocy czyli do kwadratu możemy podnosic obustronnie gdy wiemy ze obie strony są nieujemne ?

PW: Twierdzenie, że warunek 4 − x > 0 wyznacza dziedzinę jest błędem. To już jest element rozwiązania − sposób myślenia. Dziedzina to zbiór tych argumentów, dla których nierówność ma sens (nic się nie mówi, czy ma rozwiązanie). Nie miałbyś takiego pomysłu przy nierówności x² < x + 1 − dziedziną są wszystkie liczby rzeczywiste, a przecież nierówność nie ma rozwiązań dla x < −1 (tyle że tu nie musimy tak myśleć, bo mamy inne narzędzie do znajdowania rozwiązań).

tyu: tak

Jacek: No ale 4−x>0 może mówić o sensie, przecież funkcja pod pierwiastkowa może być taka, że np. dla x=R: √f(x)>2, a nie koniecznie ≥0.