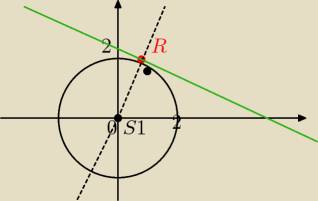
 x2 + y2 = 1
Równanie okręgu w postaci kanonicznej ma postać (x−a)2 + (y−b)2 = r2 S=(a, b) − środek
okręgu, r − promień.
(x−0)2 + (y−0)2 = 12 czyli S = (0,0) i r = 1
Znajdźmy równanie prostej k przechodzącej przez punkty R i S.
k: y = ax + b
R∊ k czyli 2 = a*1 + b
S∊ k czyli 0 = a*0 + b
Z powyższego układu otrzymujemy, że a = 2, b = 0 czyli prosta k ma postać: y = 2x.
Styczna do okręgu jest prostopadła do prostej zawierającej promień okręgu.
Szukamy równania prostej l prostopadłej do prostek k, czyli stycznej do okręgu w punkcie R.
l: y= cx + d
x2 + y2 = 1
Równanie okręgu w postaci kanonicznej ma postać (x−a)2 + (y−b)2 = r2 S=(a, b) − środek
okręgu, r − promień.
(x−0)2 + (y−0)2 = 12 czyli S = (0,0) i r = 1
Znajdźmy równanie prostej k przechodzącej przez punkty R i S.
k: y = ax + b
R∊ k czyli 2 = a*1 + b
S∊ k czyli 0 = a*0 + b
Z powyższego układu otrzymujemy, że a = 2, b = 0 czyli prosta k ma postać: y = 2x.
Styczna do okręgu jest prostopadła do prostej zawierającej promień okręgu.
Szukamy równania prostej l prostopadłej do prostek k, czyli stycznej do okręgu w punkcie R.
l: y= cx + d
| 1 | 1 | |||
k⊥l to c*2 = −1 → c= − | → y = − | x + b | ||
| 2 | 2 |
| 1 | 5 | |||
R∊l czyli 2 = − | *1 + b → b= | |||
| 2 | 2 |
| 1 | 5 | |||
Styczna do okręgu w punkcie R ma postać y = − | x + | |||
| 2 | 2 |

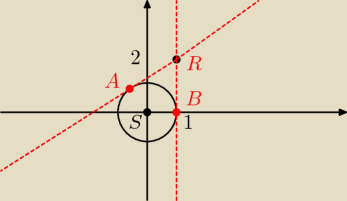 poprawiony rysunek, z tym złym było łatwiej...
poprawiony rysunek, z tym złym było łatwiej...

 Najprościej tak:
R( 1,2) i punkt przecięcia okręgu z dodatnia osia oX jest B( 1,0)
więc już mamy równanie pierwszej stycznej k: RB: x = 1
równanie drugiej stycznej wyznaczam tak:
k: y = ax +b i R€K to 2= a +b
teraz rozwiązujac układ równań prostej i okręgu nakładam warunek na Δ=0
otrzymasz: x2 ( ax+b)=1
x2 +a2x2 +2abx +b2 −1=o
(a2+1)x2 +2ab x + b2 −1=0
Δ= 4a2b2 − 4a2b2 +4a2 −4b2 +4= 4a2 −4b2 +4
to 4a2 −4b2 +4=0 => a2 −b2 = −1 i a+b =2 z poprzedniego
więc: ( a+b)(a−b)= −1 => 2(a−b) = −1
a −b = −12
a +b = 2
−−−−−−−−−
2a = 32 => a= 34 to b= 54
więc: k: y= 34x + 54 −−− to ta druga styczna
Najprościej tak:
R( 1,2) i punkt przecięcia okręgu z dodatnia osia oX jest B( 1,0)
więc już mamy równanie pierwszej stycznej k: RB: x = 1
równanie drugiej stycznej wyznaczam tak:
k: y = ax +b i R€K to 2= a +b
teraz rozwiązujac układ równań prostej i okręgu nakładam warunek na Δ=0
otrzymasz: x2 ( ax+b)=1
x2 +a2x2 +2abx +b2 −1=o
(a2+1)x2 +2ab x + b2 −1=0
Δ= 4a2b2 − 4a2b2 +4a2 −4b2 +4= 4a2 −4b2 +4
to 4a2 −4b2 +4=0 => a2 −b2 = −1 i a+b =2 z poprzedniego
więc: ( a+b)(a−b)= −1 => 2(a−b) = −1
a −b = −12
a +b = 2
−−−−−−−−−
2a = 32 => a= 34 to b= 54
więc: k: y= 34x + 54 −−− to ta druga styczna



 π
π