Geometria
YushokU:
Witam,
Mam problem z zadankiem z geometrii.
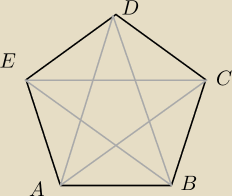
Dany jest pięciokąt wypukły ABCDE.
Udowodnij, że:
AC+BD+CE+DA+EB>AB+BC+CD+DE+EA
Myślałem, że pójdzie warunkami istnienia trójkątów, ale nie poszło, otrzymuję to wyrażenie
powiększone po lewej stronie dwukrotnie
Także proszę o wskazówki, ewentualnie rozwiązania
1 kwi 21:27
1 kwi 22:23
Qulka:
ma być 5•d>5•a więc d>a
z cosinusów
d=a√2(1+cosα)
1+cosα>0
więc ewidentnie d>a
1 kwi 22:29
YushokU: No tak, ale z twierdzenia cosinusów to mi wychodzi równość z tym 2xycosα, które się nie skraca.
I nie wiem czy dobrze zrozumiałem rozwiązanie, ale ten pięciokąt nie jest foremny, rysunek miał
mniej więcej odzwierciedlać zadanie.
1 kwi 22:38
YushokU:
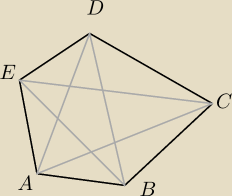
1 kwi 22:41
Qulka: po co skracać skoro ma być większe to zamiast równa się piszesz nierówność i wywalasz
1 kwi 22:52
Qulka: |AC|2>|AB|2 więc AC>AB
1 kwi 22:53
Benny: w tym poście 22:29 nie powinno być przypadkiem d=a√2(1−cosα)?
1 kwi 23:00
Qulka: ale cos dla 2 ćwiartki jest ujemny
chociaż nawet jakby był dodatni toby było większe od zera
więc tutaj to obojętne
1 kwi 23:02
Qulka: ściśle ze wzoru powinien być minus
1 kwi 23:03
Benny: Oczywiście chodziło mi o wzór, bo tak liczę i cały czas ten minus
1 kwi 23:05
Qulka: wybierz sobie α dopełniające do 180 i będziesz miał +
1 kwi 23:08
YushokU: aha, dobra, już rozumiem. Dziękuję
!
Czasem to ja się zastanawiam, jak wy wszyscy macie do mnie cierpliwość
1 kwi 23:29
YushokU: Nie, myślałem, że rozumiem, spróbowałem napisać i coś mi nie gra.
A jak pięciokąt będzie miał kąt ostry?
2 kwi 00:37