planimetria geometrykz: "W równoległobok, którego przekątne mają długości 10 i 15, wpisano romb w ten sposób, że boki rombu są równoległe do przekątnych równoległoboku. Oblicz dł. boku rombu" mój rysunek: http://postimg.org/image/cart8axw5/ z podobieństw trójkątów:

y		7,5
	=
a		10

x		5
	=
a		15

1) dobrze jest dotychczas? 2) co dalej? potrzebuję wyznaczyć y albo x − w jaki sposób?

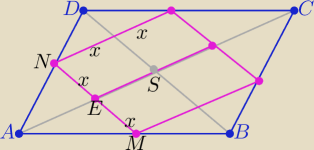
Eta: |AE|=7,5−x , |AS|=7,5 , |DB|=10 , |MN|=2x −− dł. boku rombu z Podobieństwa trójkątów AMN i ABD

|AE|		|MN|
	=		⇒ x= .... to 2x=...
|AS|		|BD|

geometrykz: skąd wiadomo, że |AE|=7,5−x? czy chodzi o to, że dwie proste równoległe przecięte przez inne proste dzielą się w takich samych proporcjach i z tego wynika |ES|=1/2 boku rombu?

Eta: Jak to skąd? ........ |AS|=7,5 . |ES|=x to |AE|= .......

geometrykz: yyyyy no to inaczej: skąd wiadomo, że |ES| to x?

Eta: A jaka jest odległość między prostymi równoległymi? ( taka sama? czy różna? Musisz wrócić do ......

geometrykz: podstawówki tak sugerowałem wcześniej, ale wolałem się upewnić dzięki, jeśli się nie obrazisz to podrzucę jeszcze jedno zadanko? niby zrobiłem a wynik się nie zgadza x(

Eta: Ja się na maturzystów nie obrażam ( tylko myślę...kogo o to zapytają na maturze w maju

geometrykz: "w trójkącie abc bok bc jest dwa razy dłuższy od boku AC, zaś bok ab ma dlugość a. punkt K należy do boku BC, przy czym |CK| : |KB|=1:3. Oblicz długość odcinka AK. obr podglądowy: http://postimg.org/image/ssqq505l7/ ABC i AKC są podobne, mają współliniową podstawę i tę samą wysokość, czyli ich pole jest w proporcji 3:1(o ile to coś tutaj daje ) czyli stosunki odpowiednich boków(cos mi sie zdaje, że tutaj się pomyliłem):

1   x 2		|AK|
	=
3   x 2		a

	a
AK=
	3

	a
odp:		czyli gdzieś mam błąd
	2

/niestety nie będzie kogo spytać ależ ja się boję tej matury.. dlatego teraz ostatni miesiąc ćwiczę planimetrię(i trochę trygonometrię, i stereometrię), choć tylko planimetria sprawia mi poważne problemy.

geometrykz: "w trójkącie abc bok BC jest dwa razy dłuższy od boku AC, zaś bok AB ma dlugość a. punkt K należy do boku BC, przy czym |CK| : |KB|=1:3. Oblicz długość odcinka AK."

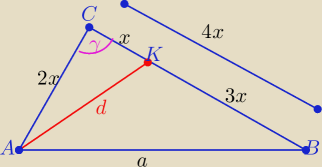
Eta: z tw. cosinusów w trójkątach AKC i ABC

	4x2+x2−d2		4x2+16x2−a2
cosγ=		i cosγ=
	2*2x*x		2*2x*4x

	a
porównując stronami otrzymasz odp: d=
	2

geometrykz: D Z I Ę K I już robię i zaraz sprawdzę

geometrykz: 10/10! wszystko ok

Eta:

kyrtap: ale czarujesz Eta z tą geometrią

geometrykz: dokładnie podziwiam! gdybym tylko miał Twoją wiedzę oraz umiejętność dostrzegania wszelkich zależności, Eta, to na mniej niż 100% nawet bym z matury nie liczył! postaram się już dzisiaj nie zawracać głowy i sobie poradzić z resztą zadań