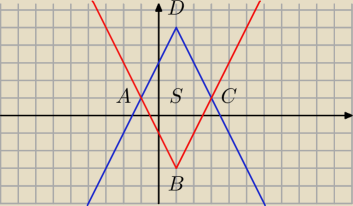
prosta maturalna geometria analityczna YushokU: Witam, Mam problem z zadaniem Właściwie to je zrobiłem. ale nie wiem jak niektóre rzeczy ładnie opisać. Oto tresc: Figura F jest określona na płaszczyźnie układem nierówności.

⎧	y≥2|x−1|−3
⎩	y≤5−2|x−1|

Oblicz stosunek pół koła zawartego w figurze F do pola tej figury. Tak je robiłem. 1.Określenie położenia punktów A i C (porównanie prostych. 2.Określenie położenia punktów B i D (tego nie wiem jak)

	1
3. Obliczenia pola ABCD		*|AC|*|BD|
	2

4.Określenie punktu S jako środka okręgu(tego nie wiem jak) 5.Obliczenie odleglości S od dowolnej prostej i opisanie tej odległosci jako promień okręgu. 6.Obliczenie Pola koła i porównanie pól. Wynik wychodzi ok, ale jak zrobić to, czego nie wiem, tak, aby zostało uznane?

Mila: 2) f(x)=2|x−1|−3 f(1)=−3 B=(1,−3) g(x)=−2|x−1|+5 g(1)=5 D=(1,5) 4) czworokąt jest rombem ⇔dwusieczne kątów wewnętrznych( zawierają przekątne) przecinają się w jednym punkcie i to jest środek okręgu wpisanego romb

	1
r=		h
	2

P=a*h masz pole to obliczenie h nie sprawi Ci kłopotu.

YushokU: Aha, czyli tylko tak z tymi punktami. Dobra, muszę jeszcze dopracować objaśnianie tego co robię, żeby na maturze nie stracić głupio punktów? Milu, czemu nie jesteś już różowa?

Eta: Za to ja jestem

Mila: Zmieniam się na wiosnę w niezapominajkę.