pomocy!
paulina: Znajdź wartości parametru p, dla których wielomian W(x) = x3 − px2 − 1 ma dokładnie
dwa miejsca zerowe.
1 kwi 17:51
paulina: ponawiam prośbę
1 kwi 18:14
ICSP: p ∊ ∅
Wielomian stopnia nieparzystego może mieć tylko nieparzystą liczbę pierwiastków.
1 kwi 19:01
paulina: ja robiłam to tak: (x−a)2(x−b)=x3−px2−1, jeden pierwiastek podwójny i jeden pojedynczy, ale
wychodziły mi z tego jakieś dziwne pierwiastki. źle myślę?
1 kwi 19:10
ICSP: jeden podwójny czyli dwa. Dodatkowo jeden pojedynczy więc łącznie dostajesz 3 pierwiastki
1 kwi 19:11
paulina: ale miejsca zerowe będą dwa, tak?
1 kwi 19:13
ICSP: Dwa różne, ale łącznie trzy.
1 kwi 19:14
pigor: ..., ale jeden może być podwójny
i w nim ekstremum =0 ; a jaką masz odpowiedź

1 kwi 19:19
pigor: ..., nie ; pierwiastek podwójny (dwukrotny) np. 0 liczy się raz

1 kwi 19:21
pigor: ..., . źle

; chodzi mi pierwiastek dwukrotny, w którym wartość W= 0 .

1 kwi 19:23
1 kwi 19:23
ICSP: Zostanę przy swoim zdaniu

1 kwi 19:26
paulina: sprawdziłam w wolframie i się zgadza, są jeszcze jakieś inne przypadki?
1 kwi 19:26
Tadeusz:
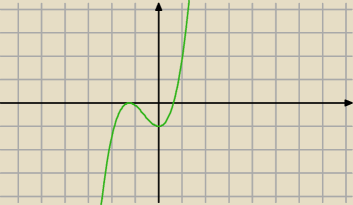
1 kwi 19:41
pigor: ... no właśnie, też mi to wyszło, ale robiłem pochodną . ...

1 kwi 19:47
Tadeusz:
można pochodną można bez
(x−a)2*(x−b) ... wymnożyć i przyrównać do W(x)
1 kwi 20:01
PW: Jeżeli nie piszą "licząc z krotnościami", to pierwiastki mogą być dwa. Pierwiastek to liczba,
nie można więc twierdzić, że np. wielomian
W(x) = (x−1)2(x+3)
ma trzy pierwiastki. Pierwiastki są dwa.
1 kwi 21:00
pigor: .. , albo po prostu zbiór 2−wuelementowy i tyle .

1 kwi 21:05
PW: Jeszcze pomarudzę: zwłaszcza że pisali w treści zadania "... ma dokładnie dwa miejsca zerowe",
a więc rozważanie krotności pierwiastków wielomianu wprowadza tylko niepotrzebny zamęt.
1 kwi 21:09


 ; chodzi mi pierwiastek dwukrotny, w którym wartość W= 0 .
; chodzi mi pierwiastek dwukrotny, w którym wartość W= 0 . 



