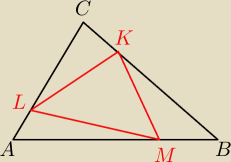
qqq karmel: Na bokach BC, CA i AB trójkata ABC wybrano punkty K, L,M takie, że

BK		CL		AM
	=		=		= k,gdzie k∊(0,+∞)
KC		LA		MB

Oblicz stosunek pola trójkata KLM do pola trójkata ABC.

	AM
		= k
	MB

AM = k* MB

AM		AM		AM		k*MB
	=		=		=		=
AB		AM + AB		AM + MB		k*MB + MB

k*MB		k
	=
MB(k+1)		k+1

	AL		1
analogicznie z		=
	AC		k+1

i dalej nie mam pomysłu co robić P_ΔKLM = P_ΔABC − P_ΔALM − P_ΔCKL − P_ΔMBK

betoniarka: ?

betoniarka:

	1		1		k		1
PAML =		AM*ALsin∡A =		*		*AB*		ACsin∡A
	2		2		k+1		k+1

może tak?

pigor: ...., tak, bardzo dobrze, czyli

	k		k
PΔAML= 12AB*ACsinA*		= PΔABC*
	(k+1)2		(1+k)2

a ponieważ analogicznie

	k
PΔAML=PΔBMK=PΔCKL= PΔABC*		, to
	(1+k)2

	k
PΔKLM= PΔABC− 3PΔABC		/ : PΔABC ⇒
	(1+k)2

	PΔKLM		k		3k
⇒		= 1− 3		= 1−		−
	PΔABC		(1+k)2		(1+k)2

	(1+k)2−3k		1−k+k2
− szukany stosunek, a dalej =		=		i tyle . ...
	(1+k)2		(1+k)2