prawdopodobieństwo warunkowe vdmath: Z grupy, w której są 4 kobiety i 6 mężczyzn, losujemy dwie osoby. Oblicz prawdopodobieństwo tego, że wylosowano dwie kobiety, jeżeli wiadomo, że wśród wylosowanych osób jest co najmniej jedna kobieta. Bardzo proszę o pomoc w rozpisaniu zdarzeń i obliczeniach.

vdmath: Mila? PW? Pomożecie? Wybaczcie, ze wywołuje, ale chyba tylko Wy podejmujecie się zadań z prawdopodobieństwa

Jacek: A − zdarzenie polegające na wylosowaniu co najmniej jednej kobiety

	4 1   6 1   4 2   * +
P(A) =
	10 2

	4 2
P(A∩B) =
	10 2

	P(A∩B)
P(B|A) =
	P(A)

Mila: Dobrze.

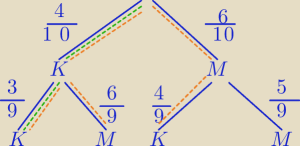
Mila: II sposób A− wylosowano co najmniej jedną kobietę A' − wylosowano 2 mężczyzn B−wylosowano dwie kobiety, jeżeli wiadomo, że wśród wylosowanych osób jest co najmniej jedna kobieta.

	6		5		30		1
P(A')=		*		=		=
	10		9		90		3

	1		2
P(A)=1−		=
	3		3

	4		3		12		2
P(A∩B)=		*		=		=
	10		9		90		15

	2   15		1
P(B/A)=		=
	2   3		5

=======================

Jacek: Czy B nie powinno być opisane jako wyłącznie wylosowanie dwóch kobiet ( bez tej wzmianki o tym, że wśród wylosowanych jest przynajmniej jedna kobieta)?

Mila: Za dużo skopiowałam. B− wylosowano dwie kobiety A wogóle to inaczej bym wszystko opisała, ale dostosowałam opis do Twojego rozwiązania, bo jest dobre. Będzie następne warunkowe, to pokażę.

vdmath: Dzięki wielkie

Mila: