rachunek
bezendu:
Ile podzbiorów ma zbiór n−elementowy ?
odpowiedź 2n
ale mając zbiór A={1,2,3} coś mi się nie zgadza
(1,2) (1,3) (2,3) (2,1) (3,2) (3,1) 6 elementów a powinno być 8
31 mar 20:49
bezendu:
I proszę o "wskazówkę" z czego to udowodnić ?
31 mar 20:50
kyrtap: {1,2,3} i jeszcze zbiór pusty
31 mar 20:50
bezendu:
Nie właśnie bo wtedy mam 10 elementów a nie 8
31 mar 20:51
Frost: Zależy czy dzielisz na niepuste podzbiory czy nie
31 mar 20:52
kyrtap: w zasadzie {1} , {2} , {3} to też są podzbiory jednoelementowe
31 mar 20:54
bezendu:
Nie, już wiem zbiór (1,3) i (3,1) to to samo itp więc teraz będzie się zgadać.Tylko jeszcze
dowód
31 mar 20:54
Janek191:
{ 1 , 2} = { 2, 1}
Brak podzbiorów jednoelementowych

31 mar 20:55
kyrtap: {1,2} , {1,3}, {2,3} ,zbiór pusty, {1,2,3} , {1}, {2},{3}
31 mar 20:55
kyrtap: {1,2 } a {2,1} to zdaję mi się że ten sam podzbiór
31 mar 20:56
Mila:
A={1,2,3}
Podzbiory:
Φ,
{1},{2},{3},
{1,2},{1,3},{2,3}
{1,2,3}
31 mar 20:57
bezendu:
Janek czyli jeszcze zbiór pusty i {2,1} a nie biorę pod uwagę nigdy podzbiorów jednoelemntowych
?
Dwa jak to udowodnić, rzuć tylko myśl, nie pisz gotowca

31 mar 20:58
bezendu:
Mila to w końcu która wersja jest poprawna ?
31 mar 20:58
Frost: Obie są takie same

31 mar 20:59
Janek191:
Napisałem, że brak Ci podzbiorów jednoelementowych, a nie, ze nie bierzemy

31 mar 21:01
Tadeusz:
{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, i pusty
31 mar 21:02
bezendu:
a teraz dowód z wzoru Newtona ?
31 mar 21:02
prosta: WITAM

jak udowodnić?
zapisać sumę podzbiorów 0−elementowych, 1−elementowych, 2−elementowych, ....
n−1 elementowych oraz n−elementowych (suma odpowiednich symboli Newtona)
i pomyślec o dwumianie Newtona

31 mar 21:04
31 mar 21:07
Mila:
| |
− liczba podzbiorów jednoelementowych |
| |
| |
−liczba podzbiorów dwuelementowych |
| |
...
.
.
Suma podzbiorów:
Lewa strona jest rozwinięciem dwumianu Newtona (a+b)
2, gdzie a=1 i b=1.
31 mar 21:07
PW: Wybierając pewne elementy do tworzonego podzbioru możemy im nadać etykietę "1" (są wybrane), a
pozostałym elementom nadać etykietę "0" (nie zostały wybrane). W ten sposoób każde utworzenie
podzbioru można utożsamić z funkcją
f: {1, 2, 3, ..., n} → {0, 1}.
W szczególności funkcja przyjmująca tylko wartości 0 jest odpowiednikiem zbioru pustego, a
funkcja przyjmująca tylko wartości 1 jest odpowiednikiem całego zbioru n−elementowego.
Powołać się na twierdzenie o liczbie takich funkcji, która jest równa 2n.
Trzeba tylko sprawdzić, czy dowód tego twierdzenia nie korzysta z twierdzenia
o liczbie podzbiorów. Jak na moją pamięć, to nie − raczej dowód jest indukcyjny.
31 mar 21:07
bezendu:
Dziękuję, zrozumiałem już

31 mar 21:08
bezendu:
Mam dwie kostki do gry, ile jest możliwości, że wypadnie co najmniej 1 szóstka
12 czy 11 ?
Nie wiem czy kostki są rozróżnialne czy nie.
1 kwi 00:25
52: 11 jak dla mnie
1 kwi 00:26
bezendu:
kwestia sporna

1 kwi 00:27
bezendu:
bo skoro (6,1) to inne zdarzenie niż (1,6) to tak
samo (6,6) (6, 6)
1 kwi 00:31
Qulka:
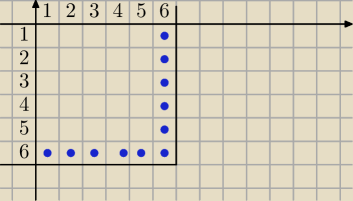
1 kwi 00:32
bezendu:
Hmm ? Ale nie ma mowy, że kostki są nierozróżnialne ? Kolejność ma znaczenie więc nie można
sobie przyjąć jednego zdarzenia (6,6) a może się mylę ?
1 kwi 00:36
Qulka: w dół to pierwsza kostka w bok druga (są rozróżnialne)
1 kwi 00:38
Jacek: To że mamy zbiór {1,2} i {6,6}, to nie znaczy, że potem możemy z tych zbiorów utworzyć tę samą
ilość wariacji. Tak to nie działa przy wariacjach z powtórzeniami.
1 kwi 00:41
bezendu:
Qulka to ile Ci wyszło ?
1 kwi 00:43
Jacek: Mamy (11,62) (61,12) oraz (61,62) − indeksy to numeracja kostek, rozróżnienie rzutów itp,
ale zawsze z tą samą kolejnością co do indeksów
1 kwi 00:48
Qulka: tak ciężko Ci policzyć kropki

11
1 kwi 00:51
Jacek: To jest jak dwukrotny rzut monetą. Mamy wariacje (OO), (RR), (OR), (RO), ale zbiory {O,R},
{R.R}. {O,O}
1 kwi 00:51
bezendu:
Policzyłem i wychodzi 11 ale czytaj co napisałem 00:31 !
1 kwi 01:02
Qulka: ale to to samo..jedna zielona 6 i jedna czerwona 6 w przeciwieństwie do zielonej 1 czerwonej 6
i czerwonej 1 zielonej 6
czy dla rozróżnienia używasz kolejności w zapisie czy kolorów to już obojętne
1 kwi 01:06
bezendu:
ok i o to mi chodziło. Dobranoc.
1 kwi 01:08
Jacek: Posługując się kolorami to zapisałbym:
(6,1) (1,6)
dla mnie to nie jest przestawienie kolejności, to jest zachowanie kolejności, czyli najpierw
czerwony, potem zielony, tylko że wynik, co do wartości, w czerwonym jest taki sam jak w
drugiej wariacji przy zielonym.
1 kwi 01:23
PW: Jak to wytłumaczyć dzieciom? Przede wszystkim zaczynamy od konstrukcji modelu matematycznego.
Czym jest pojedyncze zdarzenie elementarne? Na stole widzimy "rozrzucone bezładnie" dwie
kostki, trudno nadać im jakąś kolejność, a więc zbiór złożony z dwóch liczb jest dobrym
modelem. Żeby uniknąć dyskusji o zbiorach, w których są dwie jednakowe liczby, np. {4, 4},
przenumerujmy na chwilę liczby na jednej z kostek, np. niech zamiast 1, 2, 3, 4, 5, 6 będzie
7, 8, 8, 10, 11, 12. Teraz każdy wynik losowania jest poprawnie opisany jako zbiór złożony z
dwóch liczb, np.
{1,12} = {12,1}
jest jednym zbiorem (kolejność zapisu nie odgrywa roli, to jest ten sam zbiór będący modelem
zdarzenia elementarnego wchodzącego w skład zdarzenia "wyrzucono jedynkę i szóstkę").
Ostatecznie − modelem matematycznym pojedynczego rzutu dwiema kostkami jest zbiór złożony z
dwóch liczb, przy czym jedna z nich należy do zbioru
{1, 2, 3, 4, 5, 6},
a druga do zbioru
{7, 8, 9, 10, 11, 12}.
Jest oczywiste, że wszystkich zdarzeń jest 6·6 = 36. Taki sposób rozumowania odpowiada
sytuacji, gdy kostki są różnych kolorów − zamiast mówić o kostce zielonej i czerwonej
przenumerowaliśmy liczby na jednej z nich. Zauważmy, że wtedy zdarzenie A − "wylosowano
szóstkę i jedynkę" składa się z dwóch zdarzeń elementarnych:
A = { {1, 12}, {6, 7} },
natomiast zdarzenie B − "wylosowano dwie szóstki" jest jednoelementowe:
B = { {6,12} }.
W tym modelu odpowiedź na pytanie "Ile jest możliwości, że wypadnie co najmniej jedna szóstka"
brzmi: 11, zbiór wszystkich takich zdarzeń to
{ {1,12}, (2, 12}, {3, 12}, ..., {6, 12}, {6, 7}, {6, 8}, {6, 9},..., {6,11} }.
To są właśnie kulki tak świetnie skrótowo pokazane przez Qulkę (w jednym zbiorze 6
sztuk, w drugim też 6, dwuelementowych podzbiorów tworzonych na zasadzie "po jednej sztuce z
każdego, tak żeby była co najmniej jedna szóstka" jest 11).
A mały dociekliwy Jaś (w każdej klasie znajdzie się taki nieznośny) pyta:
− Proszę Pana, a co będzie, gdy kostki są nierozróżnialne?
Odpowiadamy mu:
− Jasiu, nie marudź. Pomaluj jedną z kostek innym kolorem, ona głupia, to się nie zorientuje.
Potem się zetrze.
1 kwi 11:54




 jak udowodnić?
zapisać sumę podzbiorów 0−elementowych, 1−elementowych, 2−elementowych, ....
n−1 elementowych oraz n−elementowych (suma odpowiednich symboli Newtona)
i pomyślec o dwumianie Newtona
jak udowodnić?
zapisać sumę podzbiorów 0−elementowych, 1−elementowych, 2−elementowych, ....
n−1 elementowych oraz n−elementowych (suma odpowiednich symboli Newtona)
i pomyślec o dwumianie Newtona 



 11
11