Geometria Czajnik: Oblicz pole, obwód, r oraz R trójkąta o wierzchołkach: A=(2,1), B=(3,3), C=(−2,3).

Frost: 1) liczysz długości boków za pomocą wektorów 2) obwód obliczasz bez problemu 3) pole możesz obliczyć z wzoru Herona

	a+b+c
4) pole trójkąta równe jest p*r gdzie p=
	2

	abc
5) R=
	4P

Czajnik: dzięki!

Czajnik: jeśli mi wyszedł taki obwód= √5 + √4 +5 to jak zapisać to pole za pomocą tego wzoru?

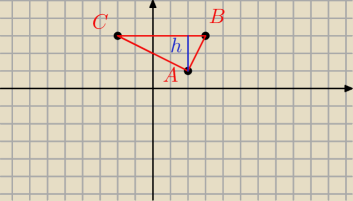
Frost: Pomyliłeś się chyba w liczenia trochę, mi boki wyszły 5, 2√5,√5 Pole obliczysz obliczając długość wysokości h, możesz odczytać z rysunku

Czajnik: okej to mam dzięki a r i R co to wgl jest i jak to obliczyć?

Janek191: Oblicz: → AB = [ 3 − 2 , 3 − 1] = [ 1 , 2] → AC = [ − 2 − 2, 3 − 1 ] = [ − 4 , 2] Pole Δ → → P = 0,5* I det AB , AC I = 0,5 *I 1*2 − 2*(−4) I = 0,5 *I 2 + 8 I = 0,5*10 = 5

Janek191: To jest Δ prostokątny , bo iloczyn skalarny wektorów → → AB o AC = [ 1, 2] o [ − 4 , 2 ] = 1*(−4) + 2*2 = 0 lub z Tw. Pitagorasa.

Frost: r− promień okręgu wpisanego R− promień okręgu opisanego

Czajnik: to jak te R i r obliczyć?

Czajnik: Wybaczcie, ale tego nie kminię

Janek191: L = a + b + c = 5 + 2√5 + √5 =5 + 3√5

	L
p =		= 2,5 + 1,5 √5
	2

P = 5 więc

	P		5
r =		=		= ...
	p		2,5 + 1,5 √5

Janek191: R = 0,5 c = 0,5* 5 = 2,5