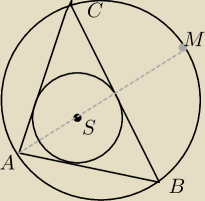
trójkąty i okręgi YushokU: Witam, Mam problem z zadaniem. W trójkącie ABC dwusieczna kąta A przecina okrąg opisany na tym trójkącie w punkcie M. Punkt S jest środkiem okręgu wpisanego w trójkąt ABC. Udowodnij, że odcinki MS, MB i MC mają tę samą długość. Jak na razie udowodniłem, że MB=MC, ale mam problem ze złapaniem MS. W ogóle nie wykorzystuję okręgu wpisanego, także proszę o nakierowanie, albo rozwiązanie Pozdrawiam i dziękuję z góry

Frost:

Frost: Jeśli udowodniłeś, że MB=MC więc |AC|=|AB| więc jeśli oznaczymy punkt styczności odcinka CB z okręgiem wpisanym jako D to odcinek AD jest środkową boku CB nie wiem czy to coś da

YushokU: Dobra, to teraz wytłumaczenie bo juz zamazałem ten rysunek jak tylko mogłem. Dwusieczna kąta MAC jest również dwusieczną BMC i z tego wynika że ΔABM iΔACM są przystające (k,b,k), lub dlatego, że są kąt C i kąt B są oparte na tej samej cięciwie. A skoro MB=MC to teraz opieram się na kątach wpisanych w . kąt MAB i MCB oparte na tym samym łuku kąty ABM i SBD są równe, bo dwusieczna Teraz obliczam kąt ASB i stwierdzam, że BSD jest równy sumie MAB i ABS, więc trójkąt MSB jest równoramienny I tutaj złapałem MS=MB=MC Ciężko to brzmi, ale nie widzę łatwiejszego rozwiązania, jakby ktoś widział to prosze

Mila: Jutro narysuję z oznaczeniami, trochę pokręciłeś. Dobranoc

Mila: Czy potrzeba jeszcze wyjaśniać?

YushokU: Nie, rozumiem Napisałem sobie to na czysto(bo tutaj rozwiązywałem zadanie, nie lubię rysować w zeszycie). i wyszło ładnie.

Mila:

YushokU: I tutaj faktycznie jest błąd, przeczytałem jeszcze raz. *kąty ABS i SBD są równe, bo dwusieczna