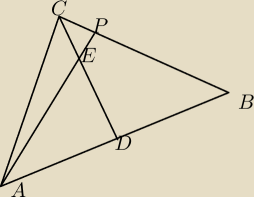
dwa ciekawe zadanka Frost: 1) ABC− dowolny trójkąt CD− środkowa boku AB AP− prosta przecinająca środkową CD w punkcie E takim, że |DE|=3 |EC| Wykazać, że |PB|=6|CP| 2) udowodnić, że prawdziwa jest nierówność:

	2
log2(πa)+log2(π+a)≥		−logππ
	logπ+a10

YushokU: 1) można twierdzeniem Cevy i twierdzeniem van Aubel'a. (warto do matury, rozwala jedną czwartą geometrii) pokażę inne rozwiązanie jak nie pójdzie ale to później, bo teraz jestem na chwilkę

Frost: Okey, właśnie zadanie pierwsze miałem na maturze próbnej w listopadzie i nikt w szkole nie zrobił... Powtarzając do matury powróciłem do tego zadania

Tadeusz:

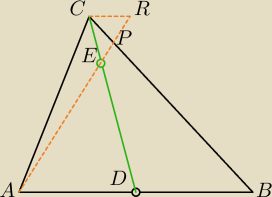
|AD|		3		|AB|		6
	=		zatem		=		jako, że |AB|=2|AD|
|CR|		1		|CR|		1

...dalej chyba jasne −

Frost: Trójkąt CRP jest podobny do ABC tak?

Tadeusz:

	2
log2(πa)+log2(π+a)≥		−logππ
	logπ+a10

(logπ+loga)²+log²(π+a)−2log(π+a)+1≥0 (logπ+loga)²+[log(π+a)−1]²≥0 i wszystko jasne −

Tadeusz: ... oczywiście, że podobny (kkk) −

Frost: a z jakiś własności wykazałeś, że kąty są równe?

Tadeusz: ∡APB=∡CPR jako kąty wierzchołkowe ∡PAB=∡CRP jako kąty naprzemianległe

Frost: no właśnie ja napisałem przez przypadek o trójkącie ABC, że jest podobny do CRP i a Ty potwierdziłeś i się tak zastanawiam jak to możliwe

Tadeusz: ... oczywiście w zadaniu 2) założenia dla a ... ale to już dla Ciebie −

Tadeusz: ... no tak trójkąty ABP i CRP oczywiście −

Frost: Założenia oczywista oczywistość Jutro sprawdzian ze stereometrii a ja siedzę na forum

Tadeusz: "narkotyk" −

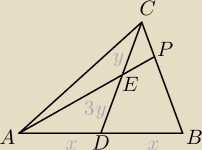
YushokU: Przepraszam, z pośpiechu źle przeczytałem to pierwsze. Ale też można je ładnie zrobić Twierdzenie Menelaosa (może Cię interesuje, albo nie, ale na pewno w przyszłości, ktoś będzie wyszukiwał to zadanie i go ten sposób zainteresuje) Twierdzenie wygląda tak http://pl.wikipedia.org/wiki/Twierdzenie_Menelaosa A tak wygląda rozwiązanie.

AB		DE		CP
	*		*		=1
AD		EC		PB

2x		3y		CP
	*		*		=1
x		y		PB

2		3		CP
	*		*		=1
1		1		PB

	CP
6*		=1
	PB

CP		1
	=
PB		6