stereometria Kasia: Podstawą ostrosłupa jest trójkąt prostokątny równoramienny.Wysokość ostrosłupa jest trzy razy dłuższa od przyprostokątnej trójkąta w podstawie, a spodek wysokości jest wierzchołkiem kąta prostego trójkąta w podstawie. Przekrój ostrosłupa płaszczyzną przechodzącą przez przeciwprostokątną podstawy i wysokość ostrosłupa jest nachylony do płaszczyzny podstawy pod kątem α takim, że tg α =√2 . Wiedząc, że pole przekroju jest równe 8√3, oblicz objętość ostrosłupa.

Kasia: ktoś pomoże?

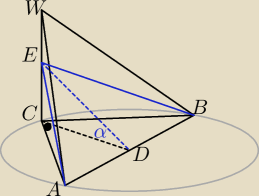
dero2005: tgα = √2 AC = CB CW = 3AC AB = AC√2

	AC
CD =		√2
	2

	sinα
tgα =		= √2
	cosα

sin2α
	= 2
cos2α

	sin2α		1−sin2α
cos2α =		=
	2		2

	√3
cosα =
	3

CD		√3
	= cosα =
DE		3

DE = CD√3

AB*DE
	= 8√3
2

AB = AC√2

	AC
CD =		√2
	2

	AC
AC√2*		√2 = 16
	2

AC² = 16 AC = 4 CW = 3AC = 12

	AC2
Pp =		= 8
	2

	Pp*CW
V =		= 32
	3

powinno być dobrze