. Bershka: Rachunek różniczkowy 1. Wyznacz te wartości parametru m dla których równanie x³−3x=m ma trzy rozwiązania. Jak to zrobić z pochodnych?

J: a dlaczego z pochodnych ?

Bershka: to zadanie mam w dziale z pochodnymi... wiem, że da się to rozłożyć i później z kwadratowej, ale chcialbym to ogarnąć pochodnymi bo może pojawić się podobne zadanie, którego nie będzie się dało pyknąć funkcją kwadratową

J: dobra ... musisz wyznaczyć ekstrema lokalne , aby określić zakres m

Bershka: ekstrema lokalne to −1 i 1 f(1) ==> m=−2 f(−1) ==> m=2 równanie ma trzy pierwiastki dla m∊(−2,2) tylko nie bardzo wiem dlaczego to oznacza, że ma 3 pierwiastki

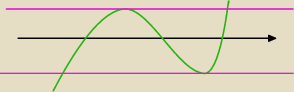
J: teraz widzisz ?

J: w tym zakresie różowa prosta o równaniu y = m , przecina wykres w trzech punktach

Bershka: ok, już wiem funkcja rosnie od −niesk do −1, maleje od −1 do 1 i znowu rosnie od 1 do +niesk, wiec 3 razy przecina os OX, tak to sobie tłumaczę heh próbowałem to teraz zrobić tym podstawowym sposobem, bez pochodnych i pustka w głowie nie mam pojęcia co zrobić z x³−3x−m=0

J: nie do końca ... zauważ,że dopóki różowa prosta jest w zakresie (−2,2) , dopóty przecina wykres w trzech punktach ( trzy rozwiazania równania ) chodzi o to, kiedy prosta przecina wykres w trzech punktach

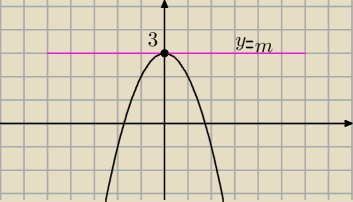
J: −x² + 3 = m dla m > 3 brak rozwiązań dla m = 3 jedno dlam < 3 dwa ... teraz czujesz ?

Bershka: tak, to drugie tak za to nie wiem skąd wziął się ten wykres wielomianowy w I sposobie, ja przyrównując 3x²−3 do zera doszedłem do paraboli x²−1=0

J: x³ − 3x = 0 ⇔ x(x²−3) = 0 ⇔ x(x − √3)(x+√3) = 0