... Bershka: Pomoże ktoś? tylko tych zadań nie zdołałam zrobić z działu geometrii analitycznej. 1. Dane są okrag o₁: x²+y²+6y+5=0 i o₂: x²+y²+8x−12y+27=0. Oblicz wspolrzedne srodka i skale jednokladnosci w ktorej obrazem okregu o₁ jest okrag o₂ 2. Punkty (1,−3) i (7,5) sa przeciwleglymi wierzcholkami rombu, ktorego pole jest rowne 100. Znajdz wspolrzedne pozostalych wierzcholkow rombu. 3. Rozwaz prostokąty, ktorych dwa wierzcholki leza na osi OX a pozostale dwa maja dodatnie rzędne i leza na paraboli y=−x²+6x. Oblicz obwod prostokata o mozliwie najwiekszym polu. 4. W rownolegloboku ABCD dane sa |AB|=6, |AD|=4, |BD|=2√10. Oblicz cosinus kąta CAD. 5. Wyznacz równania prostych zawierających dwusieczne katow utworzonych przez proste 2x−y+1=0 i x−2y+2=0

vaultboy: 1. o₁: x²+(y+3)²=4 współrzędne środka to (0,−3) promień wynosi 2 o₂: (x+4)²+(y−6)²=25 współrzędne środka to (−4,6) promień wynosi 5 Skalą jednokładności będzie stosunek promieni i wynosi on 5/2.

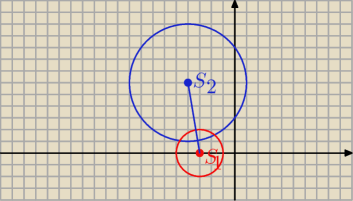
Janek191: S₁ = ( − 3, 0) S₂ = ( − 4, 6)

	r2		5
k =		=		= 2,5
	r1		2

S − środek jednokładności S = ( x , y) → S₁S₂ = [ −3 −(−4) , 6 − 0 ] = [ 1 , 6] → → S₂S = 2,5 SS₁ [ x − (−4), y − 6 ] = 2,5 *[ − 3 − x , 0 − y] [ x + 4 , y − 6 ] = [ − 7,5 − 2,5 x , − 2,5 y] x + 4 = − 7,5 − 2,5 x i y − 6 = − 2,5 y 6,5 x = − 11,5 i 3,5 y = 6

	115		60
x = −		i y =
	65		35

	23		10		12		5
x = −		= −1		i y =		= 1
	13		13		7		7

	10		5
S = ( − 1		, 1		)
	13		7

======================

Janek191: Pomyłka − powinno być 3,5 x = − 11,5

	115		23		2
x = −		= −		= − 3
	35		7		7

więc

	2		5
S = ( − 3		, 1		)
	7		7

============

J: Zad 2) 1) oblicz odległość punktów A i B 2) z pola oblicz długość drugiej przekatnej 3) oblicz środek odcinka AB 4) napsz równanie prostej AB 5) prosta prostopadła do AB przez srodek AB 6) okrąg o środku S i promieniu równym połowie drugiej przkatnej 7) punty przecięcia okręgu i drugiej prostej to szukane wierzchołki

Jacek: Janek191 może się mylę, ale skoro środek jednokładności znajduje się pomiędzy np. punktem S₁ a S₂ to czy skala jednokładności nie powinna być ujemna?

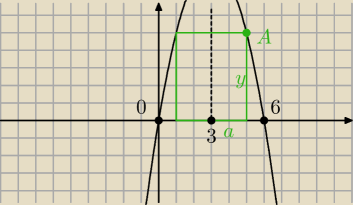
J: A(x,y) ⇔ A(x,−x²+6x) oraz a = x − 3 P = 2a*y = 2(x − 3)(−x² + 6x) .... i liczysz maksimum tej funkcji

Janek191: W tym przypadku skala jednokładności k = − 2,5 Trzeba jeszcze rozpatrzeć drugi przypadek dla k = 2,5.