Wykaż, ze ten równoległobok jest rombem Damian: Kąt ostry równoległoboku ma miare 60stopni. Stosunek długości przekątnych równoległoboku jest

	√3
równy		. Wykaż, że ten równoległobok jest rombem
	3

Nie bardzo rozumiem to stwierdzenie o przekatnych

Damian: Ktos pomoze?

Damian: Ktos pomoze?

5-latek: Oznacza to ze dlugosc mniejszse przekątnej do dlugosci wiekszsej przekątnej ma się tak jak UP{3}}{3}

Mila:

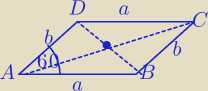
|DB|		√3
	=		⇔
|AC|		3

	√3
|DB|=|AC|*
	3

	|DB|		1
(		)2=
	|AC|		3

Z tw. cosinusów : |AC|²=a²+b²−2*a*b*cos(120^o)

	1
|AC|2=a2+b2+2a*b*
	2

|AC|²=a²+b²+ab |DB|²=a²+b²−2*a*b*cos(60^o) |BD|²=a²+b²−ab

	|DB|2		a2+b2−ab
(		=		⇔
	|AC|2		a2+b2+ab

1		a2+b2−ab
	=		⇔
3		a2+b2+ab

3a²+3b²−3ab=a²+b²+ab 2a²+2b²−4ab=0 /:2 a²+b²−2ab=0⇔ (a−b)²=0⇔ a=b⇔ Dany równoległobok jest rombem ================================